Question

Why cannot two independent monochromatic sources produce sustained interference pattern?
Deduce, with the help of Young's arrangement to produce interference pattern, an expression for the fringe width.

Answer 1

To produce a sustained interference pattern, the two sources of light must be coherent. In other words, they should emit continuous light waves (of the same wavelength or frequency) that have either the the same phase or a constant phase difference. Two independent monochromatic sources are not coherent. Hence, they cannot produce a sustained interference pattern.

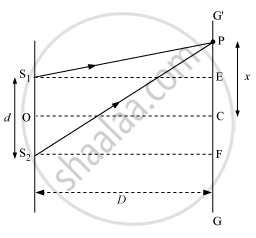
Let S₁ and S₂ be two slits separated by a distance d. GG' is the screen at a distance D from the slits S₁and S₂. Point C is equidistant from both the slits. The intensity of light will be maximum at this point because the path difference of the waves reaching this point will be zero.

At point P, the path difference between the rays coming from the slits is given by

S₁ = S₂P ‒ S₁P.

Now, 

S₁S₂ = d, EF = d and S₂F = D

∴ In ΔS₂PF,

`S_2P = [S_2F^2 + PF^2]^(1/2)`

`S_2P = [D^2+(x +d/2)^2 ]^(1/2)`

`= D [1 +D^2+((x +d/2)^2)/D^2 ]^(1/2)`

Similarly, in ΔS₁PE,

`S_1P= D [1 +((x -d/2)^2)/D^2 ]^(1/2)`

∴`S_2P-S_1P=D [1 +1/2((x + d/2)^2)/D^2 ] - D [1 +1/2((x -d/2)^2)/D^2 ]`

On expanding it binomially, we get

`S_2P - S_1P = 1/(2D)[4xd/2] =\ (xd)/D`

For bright fringes (constructive interference), the path difference is an integral multiple of wavelengths, that is, nλ.

∴ `nλ = (xd)/D`

`x =(nλD)/d`

Here,
n = 0, 1, 2, 3, 4, …

For n = 0, x₀ = 0

`n = 1, X_1 =(λD)/d `

`n = 2, X_2 =(2λD)/d `

`n = 3, X_3 =(3λD)/d `

`n = n, X_n =(nλD)/d `

Fringe Width (β) 
Separation between two consecutive bright fringes is called the width of a dark fringe.

\[\beta_1 = x_n - x_{n - 1} = \frac{\lambda D}{d}\]

Similarly, for dark fringes,

`x_n = (2n - 1)λ/2 D/d`

For `n =1,x_1 (λD)/(2d)`

For `n =2,x_2= (3λD)/(2d)`

Separation between two consecutive dark interference fringes is called the width of a bright fringe.

\[\beta_2 = x_n - x_{n - 1} = \frac{\lambda D}{d}\]

∴ β₁ = β₂

All the bright and dark fringes are of equal width, as β₁ = β₂.