Question

(i) State the essential conditions for diffraction of light.
(ii) Explain diffraction of light due to a narrow single slit and the formation of pattern of fringes on the screen.
(iii) Find the relation for width of central maximum in terms of wavelength 'λ', width of slit 'a', and separation between slit and screen 'D'.
(iv) If the width of the slit is made double the original width, how does it affect the size and intensity of the central band?

Answer 1

(i) Essential conditions for diffraction of light:

(a) Source of light should be monochromatic.
(b) Wavelength of the light used should be comparable to the size of the obstacle.
(ii) Diffraction of light due to a narrow single slit

Consider a set of parallel rays from a lens L₁ falling on a slit, form a plane wavefront. According to Huygens principle, each point on the unblocked portion of plane wave front AB sends out secondary wavelets in all directions. The secondary waves, from points equidistant from the centre C of the slit lying in the portion CA and CB of the wavefront travel the same distance in reaching O, and hence the path difference between them is zero. These secondary waves reinforce each other, resulting in maximum intensity at point O. 

Position of secondary minima
The secondary waves travelling in the direction making an angle θ with CO, will reach a point P on the screen. The intensity at P will depend on the path difference between the secondary waves emitted from the corresponding points of the wavefront. The wavelets from points A and B will have a path difference equal to BN. If this path difference is λ, then P will be a point of minimum intensity. This is because the whole wavefront can be considered to be divided into two equal halves CA and CB. If the path difference between secondary waves from A and B is λ, then the path difference between secondary waves from A and C will be λ/2, and also the path difference between secondary waves from B and C will again be λ/2. Also, for every point in the upper half AC, their is a corresponding point in the lower half CB for which the path difference between secondary waves reaching P is λ/2. Thus, at P, destructive interference will take place.

From the right-angled ΔANB given in part (ii),

BN = AB sinθ

BN = a sinθ …(1)

Suppose BN = λ and θ = θ_1.

Then, the above equation gives the following relation:

λ = a sin θ₁

_{`sin Θ_1 = λ / a    ........ (2)`}

Such a point on the screen will be the position of the first secondary minimum.

If BN = 2λ and θ = θ₂, then

_{`sin Θ_2 = (2λ) / a    ........ (3)`}

Such a point on the screen will be the position of the second secondary minimum.

In general, for n^th minimum at point P,

`sin Θ_n = (nλ) / a    ........ (4)`

Position of secondary maxima
If any other P' is such that the path difference at that point is given by

\[a\sin\theta = \frac{3\lambda}{2}\]

Then P₁ will be position of first secondary maximum. Here, we can consider the wavefront to be divided into three equal parts, so that the path difference between secondary waves from corresponding points in the 1st two parts will be λ/2. This will give rise to destructive interference. However, the secondary waves from the third part remain unused and therefore, they will reinforce each other and produce first secondary maximum. 
Similarly if the path difference at that point is given by

\[a\sin\theta = \frac{5\lambda}{2}\]

We get second secondary maxiumum of lower intensity.
In general, for nth secondary maximum, we have 

\[a\sin \theta_n = \left( 2n + 1 \right)\frac{\lambda}{2}\]

The diffraction pattern on the screen is shown below along with intensity distribution of fringes

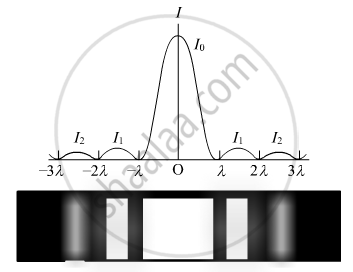
(ii) iIf y_n is the distance of the n^th minimum from the centre of the screen, then from right-angled ΔCOP,

`tanΘ_n = (OP)/(CO)`

`tanΘ_n = (y_n)/D`  ........... (5)

n case θ_n is small, sin θ_n ≈ tan θ_n

∴ From equations (iv) and (v), we get:

` (y_n)/D=(nλ)/a `

` (y_n)=(nDλ)/a `

Width of the central maximum 

\[a\sin \theta_n = \left( 2n + 1 \right)\frac{\lambda}{2}\]

\[2 y_n = \frac{2nD\lambda}{a}\]

(iv) The size of central band reduces by half according to the relation 

\[\frac{\lambda}{a}\]

Intensity of the central band will remain unchanged as the wavelength of light is same.