Advertisements
Advertisements
Question
x ∈ {real numbers} and –1 < 3 – 2x ≤ 7, evaluate x and represent it on a number line.
Solution
–1 < 3 – 2x ≤ 7
–1 < 3 – 2x and 3 – 2x ≤ 7
2x < 4 and – 2x ≤ 4
x < 2 and x ≥ – 2
Solution set = {–2 ≤ x < 2, x ∈ R}
Thus, the solution can be represented on a number line as:
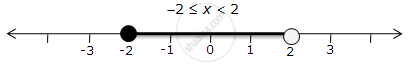
APPEARS IN
RELATED QUESTIONS
If a < b, and c > 0, then a – c > b – c where a, b, c and d are real numbers and c ≠ 0.
If the replacement set is the set of whole numbers, solve:
8 – x > 5
Given x ∈ {integers}, find the solution set of:
–5 ≤ 2x – 3 < x + 2
Given x ∈ {real numbers}, find the range of values of x for which –5 ≤ 2x – 3 < x + 2 and represent it on a number line.
Solve and graph the solution set of:
2x – 9 < 7 and 3x + 9 ≤ 25, x ∈ R
Represent the following in-equalities on real number line :
−5 < × ≤ −1
Solve for x in the following in-equation, if the replacement set is R;
3x >12
Find the solution set of the following inequalities and draw the graph of their solutions sets:
| 3 - 2x | ≥ 2
The maximum value of x for the inequation 4x ≤ 12 + x is ______.
The minimum value of x for the inequation 5x – 4 ≥ 18 – 6x is ______.
