Advertisements
Advertisements
Question
यदि APB और CQD दो समांतर रेखाएँ हैं, तो कोणों APQ, BPQ, CQP और PQD के समद्विभाजक बनाते हैं
Options
एक वर्ग
एक समचतुर्भुज
एक आयत
कोई अन्य समांतर चतुर्भुज
Solution
एक आयत
स्पष्टीकरण -
दिया गया है, APB और CQD दो समांतर रेखाएँ हैं।
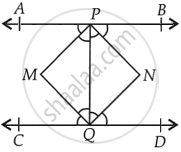
माना कोण APQ और CQP के समद्विभाजक बिंदु M पर मिलते हैं और कोण BPQ और PQD के समद्विभाजक बिंदु N पर मिलते हैं।
PM, MQ, QN और NP को मिलाइए।
चूंकि, APB || CQD
फिर, ∠APQ = ∠PQD ...[वैकल्पिक आंतरिक कोण]
⇒ ∠MPQ = 2∠NQP ...[चूँकि, PM और NQ क्रमशः ∠APQ और ∠DQP के कोण समद्विभाजक हैं।]
⇒ ∠MPQ = ∠NQP ...[दोनों पक्षों को 2 से भाग देने पर] [चूंकि, एकांतर आंतरिक कोण बराबर होते हैं।]
∴ PM || QN
इसी प्रकार, ∠BPQ = ∠CQP ...[वैकल्पिक आंतरिक कोण]
∴ PN || QM
इसलिए, चतुर्भुज PMQN एक समांतर चतुर्भुज है।
∵ ∠CQD = 180° ...[चूँकि, CQD एक रेखा है।]
⇒ ∠CQP + ∠DQP = 180°
⇒ 2∠MQP + 2∠NQP = 180° ...[चूँकि, MQ और NQ कोणों CQP और DQP के समद्विभाजक हैं।]
⇒ 2(∠MQP + ∠NQP) = 180°
⇒ ∠MQN = 90°
अत:, PMQN एक आयत है।
APPEARS IN
RELATED QUESTIONS
चतुर्भुज KLMN का एक रफ चित्र खींचिए। बताइए:
आसन्न कोणों के दो युग्म
एक आयत का एक विकर्ण उसकी एक भुजा से 25° पर नत है। इसके विकर्णों के बीच का न्यून कोण है
चतुर्भुज PQRS, की भुजाओं के मध्य-बिंदुओं को, एक ही क्रम में, मिलाने पर बना चतुर्भुज एक आयत होता है, यदि ______।
चतुर्भुज PQRS की भुजाओं के मध्य-बिंदुओं को, एक ही क्रम में मिलाने पर बना चतुर्भुज एक समचतुर्भुज होता है, यदि ______
क्या कोण 110°, 80°, 70° और 95° किसी चतुर्भुज के कोण हो सकते हैं? क्यों और क्यों नहीं?
चतुर्भुज ROPE में, आसन्न कोणों के युग्म ______ हैं।
एक समलंब में, सम्मुख भुजाओं का एक युग्म ______ होता है।
आकृति में
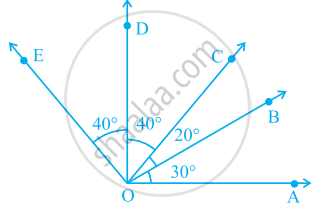
∠COA एक _____ कोण है।
आकृति में अंकित दोनों कोणों में उभयनिष्ठ बिंदुओं की संख्या ______ है।
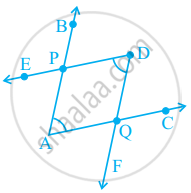
आकृति में, AE + EC क्या है?