Advertisements
Advertisements
किसी द्वैत्रिज्य की त्रिज्या 3.5 सेमी तथा उसके वृत्त चाप की लंबाई 2.2 सेमी हो तो द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए।
Concept: द्वैत्रिज्य का क्षेत्रफल (Area of a Sector)
यदि शंकु के आधार की त्रिज्या 7 सेमी तथा ऊँचाई 24 सेमी है, तो शंकु की तिरछी ऊँचाई ज्ञात कीजिए?
Concept: शंकु पृष्ठफल
7 सेमी त्रिज्या वाले गोले का पृष्ठफल ज्ञात कीजिए।
हल:
गोले का पृष्ठफल = 4πr2
= `4 xx 22/7 xx square^2`
= `4 xx 22/7 xx square`
= `square xx 7`
∴ गोले का पृष्ठफल = `square` वर्ग सेमी
Concept: गोले का पृष्ठफल
शंकु छेद के वृत्ताकार भाग की त्रिज्याएँ क्रमश: 14 सेमी तथा 6 सेमी हैं तथा उसकी ऊँचाई 6 सेमी है, तो शंकु छेद का वक्रपृष्ठफल ज्ञात कीजिए।
(π = 3.14)
Concept: शंकु छेद (Frustum of the Cone)
आइस्क्रीम का बर्तन लंबवृत्ताकर बेलन के आकार का है जिसके आधार की त्रिज्या 12 सेमी तथा ऊँचाई 7 सेमी है। यह बर्तन आइस्क्रीम से पूर्णत: भरा है। पूर्ण आइस्क्रीम विद्यार्थियों को आइस्क्रीम शंक्वाकार कोन में बांटी गई जिसके खुले भाग का व्यास 4 सेमी तथा ऊँचाई 3.5 सेमी है। यदि प्रत्येक विद्यार्थी को एक शंक्वाकार कोन दिया गया हो, तो ऐसे कितने विद्यार्थियों को आइस्क्रीम बाँटी गई?
Concept: शंकु का घनफल
किसी लंबवृत्ताकार बेलन की त्रिज्या 12 सेमी है जिसमें 20 सेमी ऊँचाई तक पानी भरा है। एक गोलाकार धातु की गेंद उसमें डुबाने पर पानी की ऊँचाई 6.75 सेमी कैसे बढ़ती है, तो उस धातु की गेंद की त्रिज्या ज्ञात कीजिए।
Concept: गोले का घनफल (Volume of Sphere)
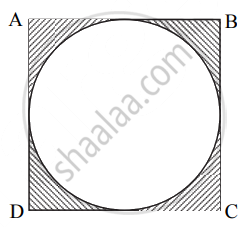
ऊपर दी गयी आकृति में `square`ABCD एक वर्ग है और एक वृत उसमें अंतर्लिखित है। वर्ग की सभी भुजायें वृत्त को स्पर्श करती हैं।
यदि AB = 14 सेमी, तो रेखांकित भाग का क्षेत्रफल ज्ञात कीजिए।
हल:
वर्ग का क्षेत्रफल = `(square)^2` ...(सूत्र)
= 142
= `square` वर्ग सेमी
∴ वृत्त का क्षेत्रफल = `square` ...(सूत्र)
= `22/7 xx 7 xx 7`
= 154 वर्ग सेमी
∴ रेखांकित भाग का क्षेत्रफल = (वर्ग का क्षेत्रफल) - (वृत्त का क्षेत्रफल)
= 196 - 154
= `square` वर्ग सेमी
Concept: वृत्तखंड (Segment of a Circle)
