Methods of solving linear equations in two variables - Determinant method

To use Cramer’s method, the equations are written as a₁x + b₁y = c1 and a₂x + b₂y = c₂.

`a_1x+b_1y=c_1`   .............(I)

`a_2x+b_2y=c_2`  ..............(II)

Here x and y are variables, a₁, b1, c1 and a2, b2, c2 are real numbers, `a_1b_2-a_2b_1ne0`

Now let us solve these equations.

Multiplying equation (I) by b₂

`a_1b_2x+b_1b_2y=c_1b_2`   ............(III)

Multiplying equation (II) by b₁.

`a_2b_1x+b_2b_1y=c_2b_1`  ..............(IV)

Subtracting equation (III) from (IV)

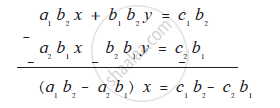
`x=(c_1b_2-c_2b_1)/(a_1b_2-a_2b_1)` ...........(V)

Similarly `y=(a_1c_2-a_2c_1)/(a_b_2-a_2b_1)` ...........(V)

To remember and write the expressions

`c_1b_2-c_2b_1, a_1b_2-a_2b_1, a_1c_2-a_2c_1` we use the determinants.

Now `a_1x+b_1y=c_1`

and `a_2x+b_2y=c_2`

We can write 3 columns `([a_1],[a_2]), ([b_1],[b_2]), ([c_1],[c_2])`

The values x, y in equation (V), (VI) are written using determinants as follows

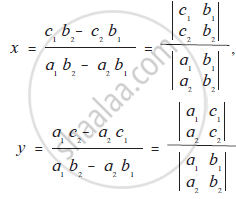
To remember let us denote

`therefore x=D_x/D, y=D_y/D`

For writting D, Dx, Dy remember the order of columns `([a_1],[a_2]), ([b_1],[b_2]), ([c_1],[c_2])` From the equations,

`a_1x+b_1y=c_1`

and `a_2x+b_2y=c_2` We get the columns `([a_1],[a_2]), ([b_1],[b_2]), ([c_1],[c_2])`

• In D the column of constants `([c_1],[c_2])` is omitted.
• In D_x the column of the coefficients of x, `([a_1],[a_2])`  is replaced by `([c_1],[c_2])`.
• In D_y the column of the coefficients of y, `([b_1],[b_2])` is replaced by  `([c_1],[c_2])`.

Using determinants, simultaneous equaions can be solved easily and in less space. This method is known as determinant method. This method was first given by a Swiss mathematician Gabriel Cramer, so it is also known as Cramer’s method.