Question

3.6 cm, 3.0 cm और 4.8 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए। सबसे छोटे कोण को समद्विभाजित कीजिए तथा प्रत्येक भाग को मापिए।

Answer 1

चरण 1 - एक किरण BX खींचिए और B को केंद्र मानकर और 4.8 cm त्रिज्या लेकर रेखा पर एक चाप काटिए और इसे C नाम दीजिए।

चरण 2 - B को केंद्र मानकर और 3.6 सेमी त्रिज्या लेकर एक चाप खींचें।

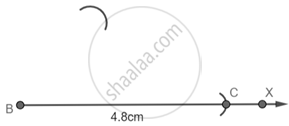
चरण 3 - C को केंद्र मानकर और 3 सेमी त्रिज्या लेकर पहले वाले चाप को A पर काटें।

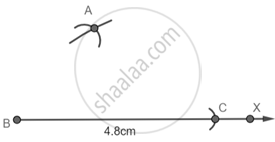
चरण 4 - AB और AC को मिलाइए।

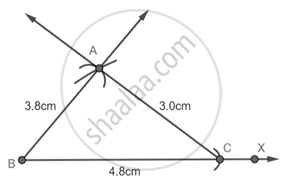
हमारा त्रिभुज निर्मित है।

अब हम जानते हैं कि त्रिभुज की सबसे छोटी भुजा का सम्मुख कोण सबसे छोटा कोण होता है।

इसलिए, ∠ABC सबसे छोटा है।

अब ∠ABC को समद्विभाजित कर रहे हैं।

चरण 5 - B को केंद्र मानकर एक चाप लगाएं जो AB और BC को क्रमश : P और Q पर काटता है।

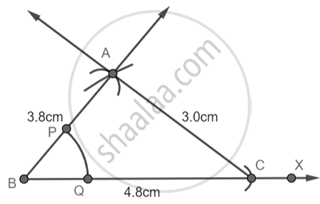
चरण 6 - P को केंद्र मानकर और PQ से अधिक त्रिज्या लेकर एक चाप लगाएं फिर Q को केंद्र मानकर और समान त्रिज्या लेकर एक अन्य चाप लगाएं जो पिछले चाप को Z पर काटता है।

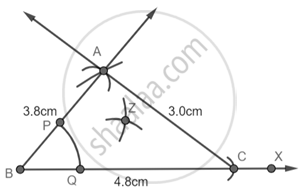
चरण 7 - BZ से जुड़ें।

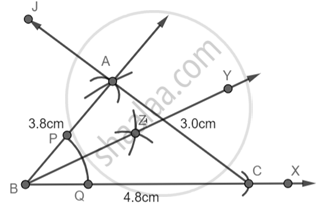
अब कोसाइन नियम से हमें पता चलता है कि ∠ABC = 40° है।

इसलिए, ∠ABY = ∠YBC = 20°।