Advertisements
Advertisements
प्रश्न
A capacitor of capacitance C is given a charge Q. At t = 0, it is connected to an ideal battery of emf ε through a resistance R. Find the charge on the capacitor at time t.
उत्तर
Given:-
Initial charge given to the capacitor = Q
When the capacitor is connected to a battery, it will charge through the battery. The initial charge will also decay.
The growth of charge across the capacitor due to the battery of emf E,
\[q = CE\left( 1 - e^{- \frac{t}{RC}} \right)\]
The decay of charge through the capacitor,
\[q' = Q e^{- \frac{t}{RC}}\]
The net charge on the capacitor at any time t,
\[q_{net} = q + q'\]
\[ = CE\left( 1 - e^{- \frac{t}{RC}} \right) + Q e^{- \frac{t}{RC}}\]
APPEARS IN
संबंधित प्रश्न
Explain what would happen if the capacitor given in previous question a 3 mm thick mica sheet (of dielectric constant = 6) were inserted between the plates,
- While the voltage supply remained connected.
- After the supply was disconnected.
Find the ratio of energy stored in the two configurations if they are both connected to the same source.
The energy density in the electric field created by a point charge falls off with the distance from the point charge as
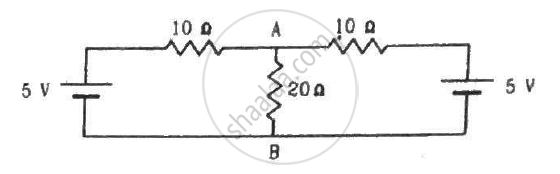
(a) Find the current in the 20 Ω resistor shown in the figure. (b) If a capacitor of capacitance 4 μF is joined between the points A and B, what would be the electrostatic energy stored in it in steady state?
A 100 μF capacitor is joined to a 24 V battery through a 1.0 MΩ resistor. Plot qualitative graphs (a) between current and time for the first 10 minutes and (b) between charge and time for the same period.
How many time constants will elapse before the current in a charging RC circuit drops to half of its initial value? Answer the same question for a discharging RC circuit.
How many time constants will elapse before the charge on a capacitors falls to 0.1% of its maximum value in a discharging RC circuit?
A capacitor with stored energy 4⋅0 J is connected with an identical capacitor with no electric field in between. Find the total energy stored in the two capacitors.
A capacitor of capacitance 100 μF is connected across a battery of emf 6 V through a resistance of 20 kΩ for 4 s. The battery is then replaced by a thick wire. What will be the charge on the capacitor 4 s after the battery is disconnected?
A point charge Q is placed at the origin. Find the electrostatic energy stored outside the sphere of radius R centred at the origin.
A metal sphere of radius R is charged to a potential V.
- Find the electrostatic energy stored in the electric field within a concentric sphere of radius 2 R.
- Show that the electrostatic field energy stored outside the sphere of radius 2 R equals that stored within it.
Answer the following question.
Obtain the expression for the energy stored in a capacitor connected across a dc battery. Hence define energy density of the capacitor
A capacitor is a device that stores ____________.
If the p. d. across a capacitor is increased from 10 V to 30 V, then the energy stored with the capacitor ____________.
A parallel plate capacitor has a uniform electric field `overset(->)("E")` in the space between the plates. If the distance between the plates is ‘d’ and the area of each plate is ‘A’, the energy stored in the capacitor is ______
(ε0 = permittivity of free space)
Prove that, if an insulated, uncharged conductor is placed near a charged conductor and no other conductors are present, the uncharged body must be intermediate in potential between that of the charged body and that of infinity.
A parallel plate capacitor (A) of capacitance C is charged by a battery to voltage V. The battery is disconnected and an uncharged capacitor (B) of capacitance 2C is connected across A. Find the ratio of total electrostatic energy stored in A and B finally and that stored in A initially.
