Advertisements
Advertisements
प्रश्न
A computers centre has four expert programmers . The centre needs four application programmes to be developed. The head of the computer centre , after stying carefully the programmes to be developed , estimates the computer time in minutes required by the respective experts to develop the application programmes as follows :
| Programmes | ||||
| Programmes | 1 | 2 | 3 | 4 |
| (Times in minutes) | ||||
| A | 120 | 100 | 80 | 90 |
| B | 80 | 90 | 110 | 70 |
| C | 110 | 140 | 120 | 100 |
| D | 90 | 90 | 80 | 90 |
How should the head of the computer centre assign the programmes to the programmers so that the total time required is minimum ?
उत्तर
After subtracting minimum value from each row:

After subtracting minimum value from each column.
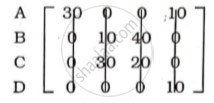
Minimum number of lines covering al zeroes
Allot the single zero· first in rows and then in column.
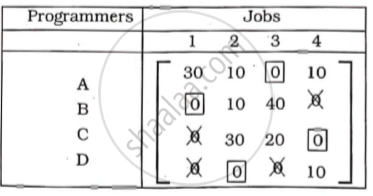
∴ Assignment
A → 3, B → 1, C→ 4. D → 2
Total minimum time
80 + 80 + 100 + 90 = 350
APPEARS IN
संबंधित प्रश्न
Solve the following equations by reduction method:
x + y + z = 6,
3x - y + 3z = 10
5x + y - 4z = 3
Find x , y , z , w if `[("x+y","x-y"),("y+z+w","2w-z")]` = `[(2,-1),(9,5)]`
If A = `[(1,2,3),(2,"a",2),(5,7,3)]` is a singular matrix , find the value of 'a'.
Find x and y if `x + y = [(7,0),(2,5)] , x - y[(3,0),(0,3)]`
Solve the following equations by reduclion method
x+3y+3z= 16 , x+4y+4z=21 , x+3y+4z = 19
If A = `[(1,-1,2),(3,0,-2),(1,0,3)]` ,
verify that A (adj A) = (adj A) A = |A| . I
If A = `[(1, 2, -3),(-3, 7, -8),(0, -6, 1)], "B" = [(9, -1, 2),(-4, 2, 5),(4, 0, -3)]` then find the matrix C such that A + B + C is a zero matrix.
If A = `[(1, -2),(3, -5),(-6, 0)],"B" = [(-1, -2),(4, 2),(1, 5)] "and C" = [(2, 4),(-1, -4),(-3, 6)]`, find the matrix X such that 3A – 4B + 5X = C.
If A = `[(7, 3, 1),(-2, -4, 1),(5, 9, 1)]`, find (AT)T.
Construct the matrix A = [aij]3×3 where aij = i − j. State whether A is symmetric or skew-symmetric.
Find matrices A and B, if 2A – B = `[(6, -6, 0),(-4, 2, 1)]` and A – 2B = `[(3, 2, 8),(-2, 1, -7)]`.
Find x and y, if `[(2x + y, -1, 1),(3, 4y, 4)] [(-1, 6, 4),(3, 0, 3)] = [(3, 5, 5),(6, 18, 7)]`.
There are two book shops own by Suresh and Ganesh. Their sales (in Rupees) for books in three subject - Physics, Chemistry and Mathematics for two months, July and August 2017 are given by two matrices A and B.
July sales (in Rupees), Physics Chemistry Mathematics
A = `[(5600, 6750, 8500),(6650, 7055, 8905)][("Suresh"), ("Ganesh")]`
August Sales (in Rupees) Physics Chemistry Mathematics
B = `[(6650, 7055, 8905),(7000, 7500, 10200)][("Suresh"), ("Ganesh")]`
Find the increase in sales in Rupees from July to August 2017.
If A = `[(5, -3),(4, -3),(-2, 1)]`, prove that (AT)T = A.
If A = `[(7, 3, 0),(0, 4, -2)], "B" = [(0, -2, 3),(2, 1, -4)]`, then find 5AT – 5BT.
If A = `[(1, 0, 1),(3, 1, 2)], "B" = [(2, 1, -4),(3, 5, -2)] "and" "C" = [(0, 2, 3),(-1, -1, 0)]`, verify that (A + 2B + 3C)T = AT + 2BT + CT.
Choose the correct alternative.
If A = `[(α, 4),(4, α)]` and |A3| = 729, then α = ______.
Fill in the blank :
If A = `[(4, x),(6, 3)]` is a singular matrix, then x is _______
Fill in the blank :
Matrix B = `[(0, 3, 1),(-3, 0, -4),("p", 4, 0)]` is skew symmetric, then the value of p is _______
State whether the following is True or False :
Every scalar matrix is unit matrix.
State whether the following is True or False :
A = `[(4, 5),(6, 1)]` is no singular matrix.
State whether the following is True or False :
If A is symmetric, then A = –AT.
State whether the following is True or False :
If A and B are square matrices of same order, then (A + B)2 = A2 + 2AB + B2.
Solve the following :
Find x, y, z if `[(2, x, 5),(3, 1, z),(y, 5, 8)]` is a symmetric matrix.
If A = `[(1, 2, -3),(-3, 7, -8),(0, -6, 1)], "B" = [(9, -1, 2),(-4, 2, 5),(4, 0, -3)]` then find the matrix C such that A + B + C is a zero matrix
Simplify, `costheta[(costheta, sintheta),(-sintheta, costheta)] + sintheta[(sintheta, -costheta),(costheta, sintheta)]`
Find x and y, if `[(2x + y, -1, 1),(3, 4y, 4)] + [(-1, 6, 4),(3, 0, 3)] = [(3, 5, 5),(6, 18, 7)]`
Evaluate: `[(3),(2),(1)][(2,-4,3)]`
Answer the following question:
If A = `[(1, -1, 0),(2, 3, 4),(0, 1, 2)]`, B = `[(2, 2, -4),(-4, 2, -4),(2, -1, 5)]`, show that BA = 6I
State whether the following statement is True or False:
`[(2, 0, 0),(3, -1, 0),(-7, 3, 1)]` is a skew symmetric matrix
If A = `[(2, 5),(1, 3)]` then A–1 = ______.
If `A = [(-3,2),(2,4)], B = [(1,a),(b,0)] "and" (A + B)(A-B) = A^2 - B^2, "Find" a "and" b`
If A = `[(5, 4),(-2, 3)]` and B = `[(-1, 3),(4, -1)]`, then find CT , such that 3A – 2B + C = I, where I is the unit matrix of order 2
