Advertisements
Advertisements
प्रश्न
A computers centre has four expert programmers . The centre needs four application programmes to be developed. The head of the computer centre , after stying carefully the programmes to be developed , estimates the computer time in minutes required by the respective experts to develop the application programmes as follows :
| Programmes | ||||
| Programmes | 1 | 2 | 3 | 4 |
| (Times in minutes) | ||||
| A | 120 | 100 | 80 | 90 |
| B | 80 | 90 | 110 | 70 |
| C | 110 | 140 | 120 | 100 |
| D | 90 | 90 | 80 | 90 |
How should the head of the computer centre assign the programmes to the programmers so that the total time required is minimum ?
उत्तर
After subtracting minimum value from each row:

After subtracting minimum value from each column.
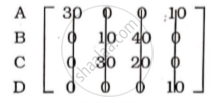
Minimum number of lines covering al zeroes
Allot the single zero· first in rows and then in column.
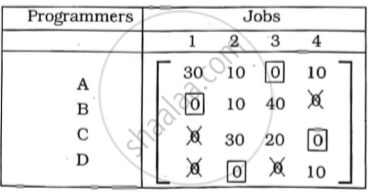
∴ Assignment
A → 3, B → 1, C→ 4. D → 2
Total minimum time
80 + 80 + 100 + 90 = 350
APPEARS IN
संबंधित प्रश्न
Find the values of x and y if
`2 [(x,5),(7,y-3)] [(3,-4),(1,2)] = [(7,6),(15,14)]`
If A = `[(1,2,3),(2,"a",2),(5,7,3)]` is a singular matrix , find the value of 'a'.
If A = `[(2, 1), (1, 1)]` show that A2 - 3A + I = 0
If A = `[(1, 2, -3),(-3, 7, -8),(0, -6, 1)], "B" = [(9, -1, 2),(-4, 2, 5),(4, 0, -3)]` then find the matrix C such that A + B + C is a zero matrix.
If A = `[(1, -2),(3, -5),(-6, 0)],"B" = [(-1, -2),(4, 2),(1, 5)] "and C" = [(2, 4),(-1, -4),(-3, 6)]`, find the matrix X such that 3A – 4B + 5X = C.
If A = `[(5, 1, -4),(3, 2, 0)]`, find (AT)T.
Find matrices A and B, if 2A – B = `[(6, -6, 0),(-4, 2, 1)]` and A – 2B = `[(3, 2, 8),(-2, 1, -7)]`.
Find x and y, if `[(2x + y, -1, 1),(3, 4y, 4)] [(-1, 6, 4),(3, 0, 3)] = [(3, 5, 5),(6, 18, 7)]`.
Find AT, if A = `[(1, 3),(-4, 5)]`
If A = `[(5, -3),(4, -3),(-2, 1)]`, prove that (AT)T = A.
If A = `[(5, 4),(-2, 3)]` and B = `[(-1, 3),(4, -1)]`, then find CT, such that 3A – 2B + C = I, whre I is e unit matrix of order 2.
If A = `[(7, 3, 0),(0, 4, -2)], "B" = [(0, -2, 3),(2, 1, -4)]`, then find AT + 4BT.
Prove that A + AT is a symmetric and A – AT is a skew symmetric matrix, where A = `[(5, 2, -4),(3, -7, 2),(4, -5, -3)]`
If A = `[(2, -1),(3, -2),(4, 1)] "and B" = [(0, 3, -4),(2, -1, 1)]`, verify that (BA)T = ATBT.
Fill in the blank:
A = `[(3),(1)]` is ........................ matrix.
Fill in the blank :
If A = `[(4, x),(6, 3)]` is a singular matrix, then x is _______
Fill in the blank :
Matrix B = `[(0, 3, 1),(-3, 0, -4),("p", 4, 0)]` is skew symmetric, then the value of p is _______
State whether the following is True or False :
Every scalar matrix is unit matrix.
State whether the following is True or False :
If A and B are square matrices of same order, then (A + B)2 = A2 + 2AB + B2.
Solve the following :
Find x, y, z if `[(2, x, 5),(3, 1, z),(y, 5, 8)]` is a symmetric matrix.
Find a, b, c if `[(1, 3/5, "a"),("b", -5, -7),(-4, "c", 0)]` is a symmetric matrix.
If A = `[(2, -3),(5, -4),(-6, 1)], "B" = [(-1, 2),(2, 2), (0, 3)] and "C" = [(4, 3),(-1, 4),(-2, 1)]` Show that (A + B) + C = A + (B + C)
Find matrices A and B, if `2"A" - "B" = [(6, -6, 0),(-4, 2, 1)] and "A" - 2"B" = [(3, 2, 8),(-2, 1, -7)]`
If A = `[("i", 2"i"),(-3, 2)] and "B" = [(2"i", "i"),(2, -3)]`, where `sqrt(-1)` = i,, find A + B and A – B. Show that A + B is a singular. Is A – B a singular ? Justify your answer.
Find x and y, if `[(2x + y, -1, 1),(3, 4y, 4)] + [(-1, 6, 4),(3, 0, 3)] = [(3, 5, 5),(6, 18, 7)]`
Answer the following question:
If A = `[(2, 1),(0, 3)]`, B = `[(1, 2),(3, -2)]`, verify that |AB| = |A||B|
Choose the correct alternative:
If A = `[(1, 3/5, x),(y, -5, -7),(-4, -7, 0)]` is a symmetric matrix, then the values of x and y are ______ respectively.
Choose the correct alternative:
`[(3, 2, 1)][(2),(-2),(-1)]` = ______
Choose the correct alternative:
If A and B are two square matrices of order 3, then (AB)T = ______
State whether the following statement is True or False:
Every square matrix of order n can be expressed as sum of symmetric and skew symmetric matrix
In a Skew symmetric matrix, all diagonal elements are ______
Find k, if A = `[(3, -2),(4, -2)]` and A2 = kA – 2I, where I is identity matrix of order 2
Find x, y, z if `{5[(0, 1),(1, 0),(1, 1)] - [(2, 1),(3, -2),(1, 3)]}[(2),(1)] = [(x + 1),(y - 1), (3z)]`
If `A = [(-3,2),(2,4)], B = [(1,a),(b,0)] "and" (A + B)(A-B) = A^2 - B^2, "Find" a "and" b`
Find the x, y, z, if `{3[(2,0),(0,2),(2,2)]-4[(1,1),(-1,2),(3,1)]}[(1),(2)]=[(x-3),(y-1),( 2z)]`
If A = `[(5, 4),(-2, 3)]` and B = `[(-1, 3),(4, -1)]`, then find CT , such that 3A – 2B + C = I, where I is the unit matrix of order 2
