Advertisements
Advertisements
प्रश्न
A game consists of tossing a one-rupee coin three times, and noting its outcome each time. Find the probability of getting at least two tails.
उत्तर
When a coin is tossed three times, all possible outcomes are
HHH, HHT, HTH, THH, HTT, THT, TTH and TTT.
Number of total outcomes = 8.
Outcomes with atleast two tails are TTH, THT, HTT and TTT.
Number of outcomes with atleast two tails = 4.
∴ P(getting at least two tails) = `("Number of favourable outcomes")/"Number of all possible outcomes"`
`= 4/8 = 1/2`
Thus, the probability of getting at least two tails is 1/2.
APPEARS IN
संबंधित प्रश्न
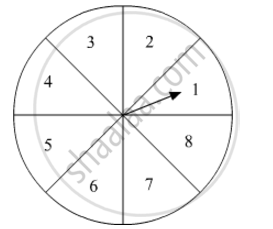
A game of chance consists of spinning an arrow on a circular board, divided into 8 equal parts, which comes to rest pointing at one of the numbers 1, 2, 3, ..., 8 (Fig. 9), which are equally likely outcomes. What is the probability that the arrow will point at (i) an odd number (ii) a number greater than 3 (iii) a number less than 9.
Two different dice are thrown together. Find the probability of getting a number greater than 3 on each die.
A bag contains cards numbered from 1 to 49. A card is drawn from the bag at random, after mixing the cards thoroughly. Find the probability that the number on the drawn card is an even prime number.
A bag contains cards numbered from 1 to 49. A card is drawn from the bag at random, after mixing the cards thoroughly. Find the probability that the number on the drawn card is a perfect square.
In a hockey team, there are 6 defenders, 4 offenders, and 1 goalee. Out of these, one player is to be selected randomly as a captain. Find the probability of the selection that – The goalee will be selected.
In a class of 42 students in Model High School, 3 students use spectacles.
Fill in the following boxes to find the probability of a students selected
at random is wearing sepctacles.
The total number of students in the class is 42.
∴n(S) = ...... ,
Let the event, a student uses spectacles, be A.
∴ n(A) = ...........
∴ P(A) = ............ ∴ P(A) = ............
The following table shows the blood-groups of employees in a bank.
Event C is : ‘the blood-group of an employee is AB.’
| Blood - group | A | B | AB | 0 |
| No. of employees | 20 | 40 | 15 | 25 |
If an employee is chosen at random, what is the probability that his blood-group is AB ?
Fill in the following boxes and find the answer
n(S)= ______
n(C)= ______
p(C)=________=_________
In a bag there are 44 identical cards with figure of circle or square on them. There are 24 circles, of which 9 are blue and rest are green and 20 squares of which 11 are blue and rest are green. One card is drawn from the bag at random. Find the probability that it has the figure of
From a well shuffled pack of cards, a card is drawn at random. Find the probability of getting a black queen.
Two coins are tossed simultaneously. Find the probability of getting exactly one head.
It is known that a box of 200 electric bulbs contains 16 defective bulbs. One bulb is taken out at random from the box. What is the probability that the bulb drawn is defective.
A box contains 25 cards numbered from 1 to 25. A card is drawn at random from the bag. Find the probability that the number on the drawn card is divisible by 2 or 3.
Cards numbered 1 to 30 are put in a bag. A card is drawn at random from the bag. Find the probability that the number on the drawn card is not divisible by 3,
All red face cards are removed from a pack of playing cards. The remaining cards are well shuffled and then a card is drawn at random from them. Find the probability that the drawn card is a card of clubs.
A game consists of tossing a coin 3 times and noting the outcome each time. If getting the same result in all the tosses is a success, find the probability of losing the game.
A coin is tossed twice. Find the probability of getting: two tails
Two coins are tossed together. Find the probability of getting: exactly one tail
Two dice are thrown at the same time. Find the probability that the sum of the two numbers appearing on the top of the dice is: less than 12
What is the probability of throwing an even number with a single standard dice of six faces?
Two dice are rolled, find the probability that the sum is equal to 4

