Advertisements
Advertisements
Question
A game consists of tossing a one-rupee coin three times, and noting its outcome each time. Find the probability of getting at least two tails.
Solution
When a coin is tossed three times, all possible outcomes are
HHH, HHT, HTH, THH, HTT, THT, TTH and TTT.
Number of total outcomes = 8.
Outcomes with atleast two tails are TTH, THT, HTT and TTT.
Number of outcomes with atleast two tails = 4.
∴ P(getting at least two tails) = `("Number of favourable outcomes")/"Number of all possible outcomes"`
`= 4/8 = 1/2`
Thus, the probability of getting at least two tails is 1/2.
APPEARS IN
RELATED QUESTIONS
A letter of English alphabet is chosen at random. Determine the probability that the chosen letter is consonant.
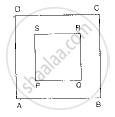
In the given figure, a square dart board is shown. The length of a side of the larger square is 1.5 times the length of a side of the smaller square. If a dart is thrown and lands on the larger square. What is the probability that it will land in the interior of the smaller square?
A box contains 20 cards numbered from 1 to 20. A card is drawn at random from the box. Find the probability that the number on the drawn card is a prime number.
Cards numbered 1 to 30 are put in a bag. A card is drawn at random from this bag. Find the probability that the number on the drawn card is a prime number greater than 7
In a bag there are 44 identical cards with figure of circle or square on them. There are 24 circles, of which 9 are blue and rest are green and 20 squares of which 11 are blue and rest are green. One card is drawn from the bag at random. Find the probability that it has the figure of
In a bag there are 44 identical cards with figure of circle or square on them. There are 24 circles, of which 9 are blue and rest are green and 20 squares of which 11 are blue and rest are green. One card is drawn from the bag at random. Find the probability that it has the figure of green colour
Two numbers 'a' and 'b' are selected successively without replacement in that order from the integers 1 to 10. The probability that\[\frac{a}{b}\] is an integer, is
Two dice are rolled together. Find the probability of getting such numbers on the two dice whose product is 12.
A jar contains 54 marbles, each of which some are blue, some are green and some are white. The probability of selecting a blue marble at random is `1/3` and the probability of selecting a green marble at random is `4/9`. How many white marbles does the jar contain?
From a well-shuffled deck of 52 cards, one card is drawn at random. What is the probability of getting a queen?
Two dice are rolled simultaneously, write down the total number of possible outcomes.
In a hockey team there are 6 defenders, 4 offenders and 1 goalee. Out of these, one player is to be selected randomly as a captain. Find the probability of the selection that – A defender will be selected.
In a certain race, there are three boys X,Y, Z. The winning probability of X is twice than Y and the winning probability of Y is twice than Z. If P(X) + P(Y) + P(Z) = 1, then find the winning probability of each girl.
A bag contains 3 white, 5 black, and 2 red balls, all of the same shape and size. A ball is drawn from the bag without looking into it, find the probability that the ball drawn is a white ball.
Three identical coins are tossed together. What is the probability of obtaining:
exactly two heads?
Frame two problems in calculating probability, based on the spinner shown here.
A coin is tossed three times. The number of possible outcomes is ______.
When a dice is thrown, outcomes 1, 2, 3, 4, 5, 6 are equally ______.
A card is drawn at random from a pack of well shuffled 52 playing cards. Complete the following activity to find the probability that the card drawn is:
Event A: The card drawn is an ace.
Event B: The card drawn is a spade.
Activity: 'S' is the sample space.
∴ n(S) = 52
Event A: The card drawn is an ace.
∴ n(A) = `square`
P(A) = `square` ......(formula)
∴ P(A) = `square/52`
∴ P(A) = `square/13`
Event B: The card drawn is a spade.
∴ n(B) = `square`
P(B) = `(n(B))/(n(S))`
∴ P(B) = `square/4`
A bag contains 25 cards, numbered through 1 to 25. A card is drawn at random. What is the probability that the number on the card drawn is a perfect square?
