Advertisements
Advertisements
प्रश्न
A girl walks 4 km towards west, then she walks 3 km in a direction 30° east of north and stops. Determine the girl’s displacement from her initial point of departure.
उत्तर
Let the headings O and B be the girl's initial and final positions. Then, the position of the girl can be shown.
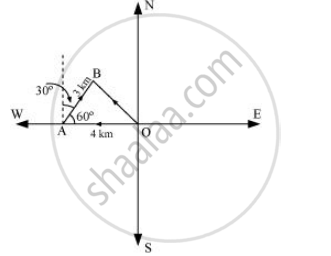
now we have:
`vec(OA) = -4hati`
`vec(AB) = hati |vec(AB)| cos60° + hatj |vec(AB)|sin60°`
= `hati xx 3 xx (1/2) + hatj xx 3 xx (sqrt3/2)`
= `(3/2)hati + ((3sqrt3)/2)hatj`
By the triangle rule of vector addition, we have:
`vec(OB) = vec(OA) + vec(AB)`
= `(-4hati) + (3/2hati + (3sqrt3)/2hatj)`
= `(-4 + 3/2)hati + (3sqrt3)/2hatj`
= `((-8 + 3)/2)hati +(3sqrt3)/2hatj`
= `(-5)/2hati + (3sqrt3)/2hatj`
Therefore, the girl's displacement from her initial point of departure is `(-5)/2hati + (3sqrt3)/2hatj`.
APPEARS IN
संबंधित प्रश्न
Find the values of x and y so that the vectors `2hati + 3hatj and xhati + yhatj` are equal.
Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (–5, 7).
In triangle ABC, which of the following is not true:

If `veca = vecb + vecc`, then is it true that `|veca| = |vecb| + |vecc|`? Justify your answer.
If `veca = hati +hatj + hatk, vecb = 2hati - hatj + 3hatk and vecc = hati - 2hatj + hatk` find a unit vector parallel to the vector `2veca - vecb + 3vecc`.
The two adjacent sides of a parallelogram are `2hati - 4hatj + 5hatk` and `hati - 2hatj - 3hatk`. Find the unit vector parallel to its diagonal. Also, find its area.
Let `veca = hati + 4hatj + 2hatk, vecb = 3hati - 2hatj + 7hatk ` and `vecc = 2hati - hatj + 4hatk`. Find a vector `vecd` which is perpendicular to both `veca` and `vecb`, and `vecc.vecd = 15`.
ABCD is a quadrilateral. Find the sum the vectors \[\overrightarrow{BA} , \overrightarrow{BC} , \overrightarrow{CD}\] and \[\overrightarrow{DA}\]
ABCDE is a pentagon, prove that
\[\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CD} + \overrightarrow{DE} + \overrightarrow{EA} = \overrightarrow{0}\]
Prove that the sum of all vectors drawn from the centre of a regular octagon to its vertices is the zero vector.
If P is a point and ABCD is a quadrilateral and \[\overrightarrow{AP} + \overrightarrow{PB} + \overrightarrow{PD} = \overrightarrow{PC}\], show that ABCD is a parallelogram.
Prove that the points \[\hat{i} - \hat{j} , 4 \hat{i} + 3 \hat{j} + \hat{k} \text{ and }2 \hat{i} - 4 \hat{j} + 5 \hat{k}\] are the vertices of a right-angled triangle.
Find the sum of the following vectors: \[\overrightarrow{a} = \hat{i} - 2 \hat{j} , \overrightarrow{b} = 2 \hat{i} - 3 \hat{j} , \overrightarrow{c} = 2 \hat{i} + 3 \hat{k} .\]
If `veca=2hati+hatj-hatk, vecb=4hati-7hatj+hatk`, find a vector \[\vec{c}\] such that \[\vec{a} \times \vec{c} = \vec{b} \text { and }\vec{a} \cdot \vec{c} = 6\].
Find the unit vector in the direction of the sum of the vectors `2hati + 3hatj - hatk and 4hati - 3hatj + 2hatk .`
Show that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.
If `6hati + 10hatj + 3hatk = x(hati + 3hatj + 5hatk) + y(hati - hatj + 5hatk) + z(hati + 3hatj - 4hatk)`, then ______
`[(bar"a", bar"b" + bar"c", bar"a" + bar"b" + bar"c")]` = ______.
Find the value of λ such that the vectors `vec"a" = 2hat"i" + lambdahat"j" + hat"k"` and `vec"b" = hat"i" + 2hat"j" + 3hat"k"` are orthogonal ______.
Let the position vectors of the points A, Band C be `veca, vecb` and `vecc` respectively. Let Q be the point of intersection of the medians of the triangle ΔABC. Then `vec(QA) + vec(QB) + vec(QC)` =
`veca, vecb` and `vecc` are perpendicular to `vecb + vecc, vecc + veca` and `veca + vecb` respectively and if `|veca + vecb|` = 6, `|vecb + vecc|` = 8 and `|vecc + veca|` = 10, then `|veca + vecb + vecc|` is equal to
A vector whose initial and terminal point continues is known as:-
Find the value of `x` and `y`. so that the vectors `2hatj + 3hatj` and `xhati + yhati` are equal
If in ΔABC, `vec(BA) = 2veca` and `vec(BC) = 3vecb`, then `vec(AC)` is ______.
