Advertisements
Advertisements
प्रश्न
A manometer reads the pressure of a gas in an enclosure as shown in Figure (a) When a pump removes some of the gas, the manometer reads as in Figure (b) The liquid used in the manometers is mercury and the atmospheric pressure is 76 cm of mercury.
(a) Give the absolute and gauge pressure of the gas in the enclosure for cases (a) and (b), in units of cm of mercury.
(b) How would the levels change in case (b) if 13.6 cm of water (immiscible with mercury) are poured into the right limb of the manometer? (Ignore the small change in the volume of the gas).

उत्तर
a) 96 cm of Hg & 20 cm of Hg; 58 cm of Hg & –18 cm of Hg
For figure (a)
Atmospheric pressure, P0 = 76 cm of Hg
Difference between the levels of mercury in the two limbs gives gauge pressure
Hence, gauge pressure is 20 cm of Hg.
Absolute pressure = Atmospheric pressure + Gauge pressure
= 76 + 20 = 96 cm of Hg
For figure (b)
Difference between the levels of mercury in the two limbs = –18 cm
Hence, gauge pressure is –18 cm of Hg.
Absolute pressure = Atmospheric pressure + Gauge pressure
= 76 cm – 18 cm = 58 cm
b) 13.6 cm of water is poured into the right limb of figure (b).
Relative density of mercury = 13.6
Hence, a column of 13.6 cm of water is equivalent to 1 cm of mercury.
Let h be the difference between the levels of mercury in the two limbs.
The pressure in the right limb is given as:
`P_R` Atmospheric pressure + 1 cm of Hg
= 76 + 1 = 77 cm of Hg … (i)
The mercury column will rise in the left limb.
Hence, pressure in the left limb, `P_L = 58 + h` ... (ii)
Equating equations (i) and (ii), we get:
77 = 58 + h
∴h = 19 cm
Hence, the difference between the levels of mercury in the two limbs will be 19 cm.
APPEARS IN
संबंधित प्रश्न
Does it matter if one uses gauge instead of absolute pressures in applying Bernoulli’s equation? Explain.
A barometer tube reads 76 cm of mercury. If the tube is gradually inclined keeping the open end immersed in the mercury reservoir, will the length of mercury column be 76 cm, more than 76 cm or less than 76 cm?
A one meter long glass tube is open at both ends. One end of the tube is dipped into a mercury cup, the tube is kept vertical and the air is pumped out of the tube by connecting the upper end to a suction pump. Can mercury be pulled up into the pump by this process?
Consider the barometer shown in the following figure. If a small hole is made at a point P in the barometer tube, will the mercury come out from this hole?
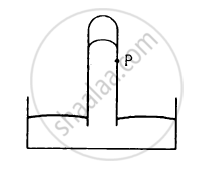
Suppose the pressure at the surface of mercury in a barometer tube is P1 and the pressure at the surface of mercury in the cup is P2.
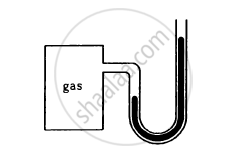
The heights of mercury surfaces in the two arms of the manometer shown in figure are 2 cm and 8 cm.
Atmospheric pressure = 1.01 × 105 N−2. Find (a) the pressure of the gas in the cylinder and (b) the pressure of mercury at the bottom of the U tube.
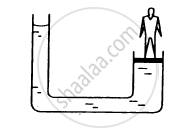
The area of cross section of the wider tube shown in figure is 900 cm2. If the boy standing on the piston weighs 45 kg, find the difference in the levels of water in the two tubes.
If water be used to construct a barometer, what would be the height of water column at standard atmospheric pressure (76 cm of mercury) ?
Water is filled in a rectangular tank of size 3 m × 2 m × 1 m. (a) Find the total force exerted by the water on the bottom surface on the tank. (b) Consider a vertical side of area 2 m × 1 m. Take a horizontal strip of width δx metre in this side, situated at a depth of x metre from the surface of water. Find the force by the water on this strip. (c) Find the torque of the force calculate in part (b) about the bottom edge of this side.
(d) Find the total force by the water on this side.
(e) Find the total torque by the water on the side about the bottom edge. Neglect the atmospheric pressure and take g = 10 ms−2.
A glass capillary sealed at the upper end is of length 0.11 m and internal diameter 2 × 10-5 m. This tube is immersed vertically into a liquid of surface tension 5.06 × 10-2 N/m. When the length x × 10-2 m of the tube is immersed in liquid then the liquid level inside and outside the capillary tube becomes the same, then the value of x is ______ m. (Assume atmospheric pressure is 1.01 × 105 `"N"/"m"^2`)
