Advertisements
Advertisements
प्रश्न
Does it matter if one uses gauge instead of absolute pressures in applying Bernoulli’s equation? Explain.
उत्तर
No
It does not matter if one uses gauge pressure instead of absolute pressure while applying Bernoulli’s equation. The two points where Bernoulli’s equation is applied should have significantly different atmospheric pressures.
APPEARS IN
संबंधित प्रश्न
A manometer reads the pressure of a gas in an enclosure as shown in Figure (a) When a pump removes some of the gas, the manometer reads as in Figure (b) The liquid used in the manometers is mercury and the atmospheric pressure is 76 cm of mercury.
(a) Give the absolute and gauge pressure of the gas in the enclosure for cases (a) and (b), in units of cm of mercury.
(b) How would the levels change in case (b) if 13.6 cm of water (immiscible with mercury) are poured into the right limb of the manometer? (Ignore the small change in the volume of the gas).

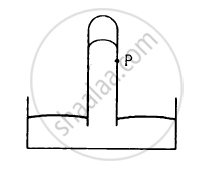
Consider the barometer shown in the following figure. If a small hole is made at a point P in the barometer tube, will the mercury come out from this hole?
The three vessels shown in the following figure have same base area. Equal volumes of a liquid are poured in the three vessels. The force on the base will be
Shows in the following figure a siphon. The liquid shown is water. The pressure difference PB − PAbetween the points A and B is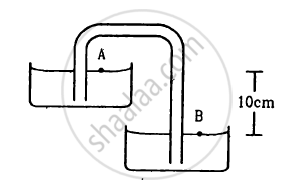
Suppose the pressure at the surface of mercury in a barometer tube is P1 and the pressure at the surface of mercury in the cup is P2.
A barometer kept in an elevator reads 76 cm when it is at rest. If the elevator goes up with increasing speed, the reading will be ______.
The weight of an empty balloon on a spring balance is W1. The weight becomes W2when the balloon is filled with air. Let the weight of the air itself be w. Neglect the thickness of the balloon when it is filled with air. Also neglect the difference in the densities of air inside and outside the balloon.
(a) W2 = W1
(b) W2 = W1 + w
(c) W2 < W1 + w
(d) W2 > W1
Suppose the glass of the previous problem is covered by a jar and the air inside the jar is completely pumped out. (a) What will be the answers to the problem? (b) Show that the answers do not change if a glass of different shape is used provided the height, the bottom area and the volume are unchanged.
Water leaks out from an open tank through a hole of area 2 mm2 in the bottom. Suppose water is filled up to a height of 80 cm and the area of cross section of the tanks is 0.4 m2. The pressure at the open surface and at the hole are equal to the atmospheric pressure. Neglect the small velocity of the water near the open surface in the tank. (a) Find the initial speed of water coming out of the hole. (b) Find the speed of water coming out when half of water has leaked out. (c) Find the volume of eater leaked out using a time interval dt after the height remained is h. Thus find the decrease in height dh in terms of h and dt.
(d) From the result of park (c) find the time required for half of the water to leak out.
A glass capillary sealed at the upper end is of length 0.11 m and internal diameter 2 × 10-5 m. This tube is immersed vertically into a liquid of surface tension 5.06 × 10-2 N/m. When the length x × 10-2 m of the tube is immersed in liquid then the liquid level inside and outside the capillary tube becomes the same, then the value of x is ______ m. (Assume atmospheric pressure is 1.01 × 105 `"N"/"m"^2`)
