Advertisements
Advertisements
प्रश्न
A matchbox is 4 cm long, 2.5 cm broad, and 1.5 cm in height. Its outer sides are to be covered exactly with craft paper. How much paper will be required to do so?
उत्तर
Length of the matchbox, l = 4 cm
Breadth of the matchbox, b = 2.5 cm
Height of the matchbox, h = 1.5 cm
∴ Surface area of the box
= 2(l × b + b × h + h × l)
= 2(4 × 2.5 + 2.5 × 1.5 + 1.5 × 4)
= 2(10 + 3.75 + 6)
= 2 × 19.75
= 39.5 cm2
Hence, 39.5 cm2 of the craft paper will be needed to cover the matchbox.
संबंधित प्रश्न
A plastic box 1.5 m long, 1.25 m wide and 65 cm deep, is to be made. It is to be open at the top. Ignoring the thickness of the plastic sheet, determine:
(i) The area of the sheet required for making the box.
(ii) The cost of sheet for it, if a sheet measuring 1 m2 costs Rs 20.
The length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost
of white washing the walls of the room and the ceiling at the rate of Rs. 7.50 m2.
A village, having a population of 4000, requires 150 litres water per head per day. It has a tank which is 20 m long, 15 m broad and 6 m high. For how many days will the water of this tank last?
A classroom is 7 m long, 6 m broad and 3.5 m high. Doors and windows occupy an area of 17 m2. What is the cost of white-washing the walls at the rate of Rs 1.50 per m2.
The external dimensions of a closed wooden box are 48 cm, 36 cm, 30 cm. The box is made of 1.5 cm thick wood. How many bricks of size 6 cm × 3 cm × 0.75 cm can be put in this box?
The number of cubes of side 3 cm that can be cut from a cuboid of dimensions 10 cm × 9 cm × 6 cm, is ______.
On a particular day, the rain fall recorded in a terrace 6 m long and 5 m broad is 15 cm. The quantity of water collected in the terrace is
The length, breadth, and height of a cuboid (rectangular solid) are 4 : 3: 2.
(i) If its surface area is 2548 cm2, find its volume.
(ii) If its volume is 3000 m3, find its surface area.
The length breadth and height of a cuboid are in the ratio of 3 : 3 : 4. Find its volume in m3 if its diagonal is `5sqrt(34)"cm"`.
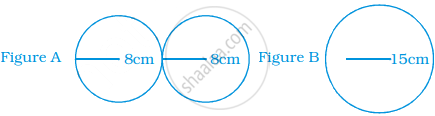
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?