Advertisements
Advertisements
प्रश्न
A medicine capsule is in the shape of a cylinder of diameter 0.5 cm with a hemisphere tucked at each end. The length of the entire capsule is 2 cm. The capacity of the capsule is
उत्तर
0.36 cm3
Radius of the capsule `= 0.5/2 "cm"`
= 0.25 cm
Let the length of the cylindrical part of the capsule be x cm.
Then,
0.25 + x + 0.25 = 2
⇒ 0.5 + x = 2
⇒ x = 1.5
Hence, the capacity of the capsule
= 2 × (Volume of the hemisphere) + (Volume of the cylinder)
`=(2xx2/3pi"r")^3+pi"r"^2"h"`
`=(4/3xx22/7xx1/4xx1/4)+(22/7xx1/4xx1/4xx1.5)` `["since" 0.25 =1/4] `
`=(11/168 + 33/112) "cm"^3`
`=121/336 "cm"^3 = 0.36 "cm"^3`
APPEARS IN
संबंधित प्रश्न
A metal parallelopiped of measures 16 cm x 11 cm x 10 cm was melted to make coins. How many coins were made if the thickness and diameter of each coin were 2 mm and 2 cm respectively?
A tank of cylindrical shape has radius 2.8 m and its height 3.5 m. Complete the activity to find how many litres of water the tank will contain.
Capacity of water tank = Volume of cylindrical tank
= πr2h
A spherical shell of lead, whose external diameter is 18 cm, is melted and recast into a right circular cylinder, whose height is 8 cm and diameter 12 cm. Determine the internal diameter of the shell.
The radius of the base of a right circular cone of semi-vertical angle α is r. Show that its volume is \[\frac{1}{3} \pi r^3\] cot α and curved surface area is πr2 cosec α.
Two right circular cylinders of equal volumes have their heights in the ratio 1 : 2. What is the ratio of their radii ?
A cylindrical vessel 32 cm high and 18 cm as the radius of the base, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, the radius of its base is
A 5-m-wide cloth is used to make a conical tent of base diameter 14 m and height 24 m. Find the cost of cloth used, at the rate of ₹25 per metre.
From a solid cylinder whose height is 15 cm and diameter 16 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid. (Use π = 3.14)
Tick the object which has more volume
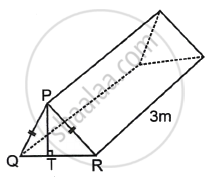
A tent is a shape of a triangular 'prism' resting on a rectangular side PQ = PR, PT = 1.5 m, QR = 1.8 m, length of the tent = 3 m. Find:
- ∠PQR
- The volume of the tent