Advertisements
Advertisements
प्रश्न
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m.
Calculate:
- the total area of the internal surface, excluding the base;
- the internal volume of the container in m3.
उत्तर
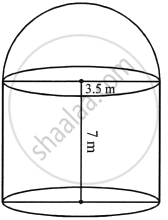
Radius of the cylinder = 3.5 m
Height = 7 m
i. Total surface area of container excluding the base = Curved surface area of the cylinder + Area of hemisphere
= `2pirh + 2pir^2`
= `(2 xx 22/7 xx 3.5 xx 7) + (2 xx 22/7 xx 3.5 xx 3.5)`
= 154 + 77 m2
= 231 m2
ii. Volume of the container = `pir^2h + 2/3pir^3`
= `(22/7 xx 3.5 xx 3.5 xx 7) + (2/3 xx 22/7 xx 3.5 xx 3.5 xx 3.5)`
= `539/2 + 539/6`
= `(1617 + 539)/6`
= `2156/6`
= 359.33 m3
संबंधित प्रश्न
If the lateral surface of a cylinder is 94.2 cm2 and its height is 5 cm, then find (i) radius of its base (ii) its volume. [Use π = 3.14]
A wooden toy is in the shape of a cone mounted on a cylinder as shown alongside. If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm; find the total surface area of the toy. [Take π = 3.14]
Find the volume of the cylinder if the circumference of the cylinder is 132 cm and height is 25 cm.
3080 cm3 of water is required to fill a cylindrical vessel completely and 2310 cm3 of water is required to fill it upto 5 cm below the top. Find :
- radius of the vessel.
- height of the vessel.
- wetted surface area of the vessel when it is half-filled with water.
Two right circular solid cylinders have radii in the ratio 3 : 5 and heights in the ratio 2 : 3. Find the ratio between their curved surface areas.
If the radius of the base of a right circular cylinder is halved keeping the same height, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is
If the radius of a cylinder is doubled and height is halved, the volume will be doubled.
Two cylinders of same volume have their radii in the ratio 1 : 6, then ratio of their heights is ______.
How many cubic metres of earth must be dug to construct a well 7 m deep and of diameter 2.8 m?
Radius of a cylinder is r and the height is h. Find the change in the volume if the height is doubled and the radius is halved.
