Advertisements
Advertisements
प्रश्न
A metre-long tube open at one end, with a movable piston at the other end, shows resonance with a fixed frequency source (a tuning fork of frequency 340 Hz) when the tube length is 25.5 cm or 79.3 cm. Estimate the speed of sound in air at the temperature of the experiment. The edge effects may be neglected.
उत्तर १
Frequency of the turning fork, ν = 340 Hz
Since the given pipe is attached with a piston at one end, it will behave as a pipe with one end closed and the other end open, as shown in the given figure.
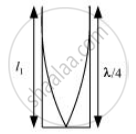
Such a system produces odd harmonics. The fundamental note in a closed pipe is given by the relation:
`l_1 = lambda/4`
Where,
Length of the pipe, `l_1 = 25.5 cm = 0.255 m`
`:.lambda = 4l_1 = 4xx 0.255 = 1.02 m`
The speed of sound is given by the relation: `v = vlambda` = 340 × 1.02 = 346.8 m/s
उत्तर २
Frequency of nth mode of vibration of the closed organ pipe of lenght
`l_1 = (2n - 1) v/(4l_1)`
Frequency of (n+1) th mode of vibration of closed pipe of length
`'l_2' = [2(n+1)-1] v/(4l_2) = (2n + 1) v/(4l_2)`
Both the modes are given to resonate with a frequency of 340 Hz.
`:. (2n - 1) v/(4l_1) = (2n+1) v/(4l_2)`
or `(2n -1)/(2n+2) = l_1/l_2 = 25.5/79.3 = 1/3`
[Approximation has been used because edge effect is being ignored. Moreover, we know that in the case of a closed organ pipe, the second resonance length is three times the first resonance length.]
On simplification, n = 1
Now, (2n-1)υ/4l1 = 340. Substituting values
(2 x 1 -1) υ x 100/4 x 25.5 = 340 or υ =346.8 ms-1
APPEARS IN
संबंधित प्रश्न
You have learnt that a travelling wave in one dimension is represented by a function y= f (x, t)where x and t must appear in the combination x – v t or x + v t, i.e. y = f (x ± v t). Is the converse true? Examine if the following functions for y can possibly represent a travelling wave:
(a) `(x – vt )^2`
(b) `log [(x + vt)/x_0]`
(c) `1/(x + vt)`
(i) For the wave on a string described in Exercise 15.11, do all the points on the string oscillate with the same (a) frequency, (b) phase, (c) amplitude? Explain your answers. (ii) What is the amplitude of a point 0.375 m away from one end?
A sonometer wire of length l vibrates in fundamental mode when excited by a tuning fork of frequency 416. Hz. If the length is doubled keeping other things same, the string will ______.
A wave travelling on a string at a speed of 10 m s−1 causes each particle of the string to oscillate with a time period of 20 ms. (a) What is the wavelength of the wave? (b) If the displacement of a particle of 1⋅5 mm at a certain instant, what will be the displacement of a particle 10 cm away from it at the same instant?
Two long strings A and B, each having linear mass density
\[1 \cdot 2 \times {10}^{- 2} kg m^{- 1}\] , are stretched by different tensions 4⋅8 N and 7⋅5 N respectively and are kept parallel to each other with their left ends at x = 0. Wave pulses are produced on the strings at the left ends at t = 0 on string A and at t = 20 ms on string B. When and where will the pulse on B overtake that on A?
The equation for the vibration of a string, fixed at both ends vibrating in its third harmonic, is given by
\[y = \left( 0 \cdot 4 cm \right) \sin\left[ \left( 0 \cdot 314 {cm}^{- 1} \right) x \right] \cos \left[ \left( 600\pi s^{- 1} \right) t \right]\]
(a) What is the frequency of vibration? (b) What are the positions of the nodes? (c) What is the length of the string? (d) What is the wavelength and the speed of two travelling waves that can interfere to give this vibration?
An organ pipe of length 0.4 m is open at both ends. The speed of sound in the air is 340 m/s. The fundamental frequency is ______
A string 1 m long is fixed at one end. The other end is moved up and down with a frequency of 20 Hz. Due to this, a stationary wave with four complete loops gets produced on the string. Find the speed of the progressive wave which produces the stationary wave.
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air increases with temperature.
Sound waves of wavelength λ travelling in a medium with a speed of v m/s enter into another medium where its speed is 2v m/s. Wavelength of sound waves in the second medium is ______.
