Advertisements
Advertisements
प्रश्न
A metre-long tube open at one end, with a movable piston at the other end, shows resonance with a fixed frequency source (a tuning fork of frequency 340 Hz) when the tube length is 25.5 cm or 79.3 cm. Estimate the speed of sound in air at the temperature of the experiment. The edge effects may be neglected.
उत्तर १
Frequency of the turning fork, ν = 340 Hz
Since the given pipe is attached with a piston at one end, it will behave as a pipe with one end closed and the other end open, as shown in the given figure.
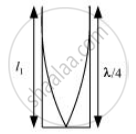
Such a system produces odd harmonics. The fundamental note in a closed pipe is given by the relation:
`l_1 = lambda/4`
Where,
Length of the pipe, `l_1 = 25.5 cm = 0.255 m`
`:.lambda = 4l_1 = 4xx 0.255 = 1.02 m`
The speed of sound is given by the relation: `v = vlambda` = 340 × 1.02 = 346.8 m/s
उत्तर २
Frequency of nth mode of vibration of the closed organ pipe of lenght
`l_1 = (2n - 1) v/(4l_1)`
Frequency of (n+1) th mode of vibration of closed pipe of length
`'l_2' = [2(n+1)-1] v/(4l_2) = (2n + 1) v/(4l_2)`
Both the modes are given to resonate with a frequency of 340 Hz.
`:. (2n - 1) v/(4l_1) = (2n+1) v/(4l_2)`
or `(2n -1)/(2n+2) = l_1/l_2 = 25.5/79.3 = 1/3`
[Approximation has been used because edge effect is being ignored. Moreover, we know that in the case of a closed organ pipe, the second resonance length is three times the first resonance length.]
On simplification, n = 1
Now, (2n-1)υ/4l1 = 340. Substituting values
(2 x 1 -1) υ x 100/4 x 25.5 = 340 or υ =346.8 ms-1
APPEARS IN
संबंधित प्रश्न
Show that the particle speed can never be equal to the wave speed in a sine wave if the amplitude is less than wavelength divided by 2π.
A wave pulse, travelling on a two-piece string, gets partially reflected and partially transmitted at the junction. The reflected wave is inverted in shape as compared to the incident one. If the incident wave has wavelength λ and the transmitted wave λ'
Two sine waves travel in the same direction in a medium. The amplitude of each wave is A and the phase difference between the two waves is 120°. The resultant amplitude will be
A travelling wave is produced on a long horizontal string by vibrating an end up and down sinusoidally. The amplitude of vibration is 1⋅0 and the displacement becomes zero 200 times per second. The linear mass density of the string is 0⋅10 kg m−1 and it is kept under a tension of 90 N. (a) Find the speed and the wavelength of the wave. (b) Assume that the wave moves in the positive x-direction and at t = 0, the end x = 0 is at its positive extreme position. Write the wave equation. (c) Find the velocity and acceleration of the particle at x = 50 cm at time t = 10 ms.
A string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160 N m−1 and is stretched by 1⋅0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring?
Two long strings A and B, each having linear mass density
\[1 \cdot 2 \times {10}^{- 2} kg m^{- 1}\] , are stretched by different tensions 4⋅8 N and 7⋅5 N respectively and are kept parallel to each other with their left ends at x = 0. Wave pulses are produced on the strings at the left ends at t = 0 on string A and at t = 20 ms on string B. When and where will the pulse on B overtake that on A?
A 2⋅00 m-long rope, having a mass of 80 g, is fixed at one end and is tied to a light string at the other end. The tension in the string is 256 N. (a) Find the frequencies of the fundamental and the first two overtones. (b) Find the wavelength in the fundamental and the first two overtones.
The string of a guitar is 80 cm long and has a fundamental frequency of 112 Hz. If a guitarist wishes to produce a frequency of 160 Hz, where should the person press the string?
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of 0.5 m.
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of `λ/2`.
