Advertisements
Advertisements
प्रश्न
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of `λ/2`.
उत्तर १
Equation for a travelling harmonic wave is given as:
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
= 2.0 cos (20πt – 0.016πx + 0.70 π)
Where,
Propagation constant, k = 0.0160 π
Amplitude, a = 2 cm
Angular frequency, ω= 20 π rad/s
Phase difference is given by the relation:
`phi = "k"x = (2pi)/lambda`
For `x = lambda/2`
`phi = (2phi)/lambda xx lambda/2`
`= pi " rad"`
उत्तर २
The given equation can be drawn be rewritten as under
y(x, t) `= 2.0 cos [2pi (10"t" - 0.0080x) + 2pi xx 0.35]`
or y(x, t) `= 2.0 cos [2pi xx 0.0080((10"t")/0.0080 - x) + 0.7pi]`
Comparing this equation with the standard equation of a travelling harmonic wave.
`(2pi)/lambda = 2pi xx 0.0080` or `lambda = 1/0.0080 " cm" = 125` cm
The phase difference between oscillatory motion of two points seperated by a distance `trianglex` is given by
`trianglephi = (2pi)/lambda trianglex`
When `trianglex = lambda/2 = 125/2` cm , then
`triangle phi = (2phi)/125 xx 125/2`
`= pi " rad"`
APPEARS IN
संबंधित प्रश्न
A bat emits an ultrasonic sound of frequency 1000 kHz in the air. If the sound meets a water surface, what is the wavelength of the transmitted sound? The speed of sound in air is 340 m s–1 and in water 1486 m s–1.
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45 Hz. The mass of the wire is 3.5 × 10–2 kg and its linear mass density is 4.0 × 10–2 kg m–1. What is (a) the speed of a transverse wave on the string, and (b) the tension in the string?
Show that for a wave travelling on a string
\[\frac{y_{max}}{\nu_{max}} = \frac{\nu_{max}}{\alpha_{max}},\]
where the symbols have usual meanings. Can we use componendo and dividendo taught in algebra to write
\[\frac{y_{max} + \nu_{max}}{\nu_{max} - \nu_{max}} = \frac{\nu_{max} + \alpha_{max}}{\nu_{max} - \alpha_{max}}?\]
A wave pulse, travelling on a two-piece string, gets partially reflected and partially transmitted at the junction. The reflected wave is inverted in shape as compared to the incident one. If the incident wave has wavelength λ and the transmitted wave λ'
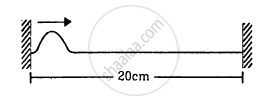
A string of length 20 cm and linear mass density 0⋅40 g cm−1 is fixed at both ends and is kept under a tension of 16 N. A wave pulse is produced at t = 0 near an ends as shown in the figure, which travels towards the other end. (a) When will the string have the shape shown in the figure again? (b) Sketch the shape of the string at a time half of that found in part (a).
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air is independent of pressure.
A bat emits an ultrasonic sound of frequency 1000 kHz in the air. If the sound meets a water surface, what is the wavelength of the the reflected sound? The speed of sound in air is 340 m s–1 and in water 1486 m s–1.
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of 4 m.
Speed of sound wave in air ______.
An engine is approaching a cliff at a constant speed. When it is at a distance of 0.9 km from cliff it sounds a whistle. The echo of the sound is heard by the driver after 5 seconds. Velocity of sound in air is equal to 330 ms-1. The speed of the engine is ______ km/h.
