Advertisements
Advertisements
प्रश्न
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45 Hz. The mass of the wire is 3.5 × 10–2 kg and its linear mass density is 4.0 × 10–2 kg m–1. What is (a) the speed of a transverse wave on the string, and (b) the tension in the string?
उत्तर १
a) Mass of the wire, m = 3.5 × 10–2 kg
Linear mass density, `mu = m/l = 4.0 xx 10^(-2) kg m^(-1)`
Frequency of vibration, ν = 45 Hz
:. Length of the wire, `l = m/mu = (3.5xx10^(-2))/(4.0xx10^(-2)) = 0.875 m`
The wavelength of the stationary wave (λ) is related to the length of the wire by the relation:
`lambda = (2l)/n`
Where n = number of nodes in the wire
For fundamental node, n = 1:
λ = 2l
λ = 2 × 0.875 = 1.75 m
The speed of the transverse wave in the string is given as:
v = νλ= 45 × 1.75 = 78.75 m/s
b) The tension produced in the string is given by the relation:
T = v2µ
= (78.75)2 × 4.0 × 10–2 = 248.06 N
उत्तर २
Here n= 45 Hz, M = `3.5 xx 10^(-2)` kg
Mass per unit length = `m = 4.0 xx 10^(-2) kg m^(-1)`
`:. l = M/m = (3.5xx10^(-2))/(4.0xx10^(-2)) = 7/8`
As `l/2 = lambda = 7/8 :. lambda = 7/4 m = 1.75 m`
a) The speed of the transverse wave,` v = vlambda = 45 xx 1.75 = 78.75 "m/s"`
b) As ` v = sqrt(T/m)`
`:. T = v^2xx m = (78.75)^2xx 4.0 xx 10^(-2) = 248.06 N`
APPEARS IN
संबंधित प्रश्न
You have learnt that a travelling wave in one dimension is represented by a function y= f (x, t)where x and t must appear in the combination x – v t or x + v t, i.e. y = f (x ± v t). Is the converse true? Examine if the following functions for y can possibly represent a travelling wave:
(a) `(x – vt )^2`
(b) `log [(x + vt)/x_0]`
(c) `1/(x + vt)`
A train, standing in a station-yard, blows a whistle of frequency 400 Hz in still air. The wind starts blowing in the direction from the yard to the station with at a speed of 10 m s–1. What are the frequency, wavelength, and speed of sound for an observer standing on the station’s platform? Is the situation exactly identical to the case when the air is still and the observer runs towards the yard at a speed of 10 m s–1? The speed of sound in still air can be taken as 340 m s–1.
The equation of a wave travelling on a string is \[y = \left( 0 \cdot 10 \text{ mm } \right) \sin\left[ \left( 31 \cdot 4 m^{- 1} \right)x + \left( 314 s^{- 1} \right)t \right]\]
(a) In which direction does the wave travel? (b) Find the wave speed, the wavelength and the frequency of the wave. (c) What is the maximum displacement and the maximum speed of a portion of the string?
A wave travels along the positive x-direction with a speed of 20 m s−1. The amplitude of the wave is 0⋅20 cm and the wavelength 2⋅0 cm. (a) Write the suitable wave equation which describes this wave. (b) What is the displacement and velocity of the particle at x= 2⋅0 cm at time t = 0 according to the wave equation written? Can you get different values of this quantity if the wave equation is written in a different fashion?
A wave travelling on a string at a speed of 10 m s−1 causes each particle of the string to oscillate with a time period of 20 ms. (a) What is the wavelength of the wave? (b) If the displacement of a particle of 1⋅5 mm at a certain instant, what will be the displacement of a particle 10 cm away from it at the same instant?
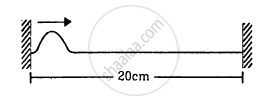
A string of length 20 cm and linear mass density 0⋅40 g cm−1 is fixed at both ends and is kept under a tension of 16 N. A wave pulse is produced at t = 0 near an ends as shown in the figure, which travels towards the other end. (a) When will the string have the shape shown in the figure again? (b) Sketch the shape of the string at a time half of that found in part (a).
A travelling wave is produced on a long horizontal string by vibrating an end up and down sinusoidally. The amplitude of vibration is 1⋅0 and the displacement becomes zero 200 times per second. The linear mass density of the string is 0⋅10 kg m−1 and it is kept under a tension of 90 N. (a) Find the speed and the wavelength of the wave. (b) Assume that the wave moves in the positive x-direction and at t = 0, the end x = 0 is at its positive extreme position. Write the wave equation. (c) Find the velocity and acceleration of the particle at x = 50 cm at time t = 10 ms.
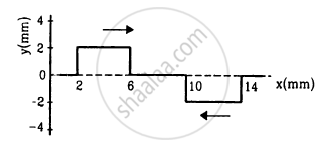
Following figure shows two wave pulses at t = 0 travelling on a string in opposite directions with the same wave speed 50 cm s−1. Sketch the shape of the string at t = 4 ms, 6 ms, 8 ms, and 12 ms.
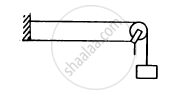
Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
At what temperatures (in °C) will the speed of sound in air be 3 times its value at O°C?
