Advertisements
Advertisements
प्रश्न
A train, standing in a station-yard, blows a whistle of frequency 400 Hz in still air. The wind starts blowing in the direction from the yard to the station with at a speed of 10 m s–1. What are the frequency, wavelength, and speed of sound for an observer standing on the station’s platform? Is the situation exactly identical to the case when the air is still and the observer runs towards the yard at a speed of 10 m s–1? The speed of sound in still air can be taken as 340 m s–1.
Advertisements
उत्तर १
The travelling harmonic wave is y(x, t) = `7.5 sin (0.0050x+ 12t + pi/4)`
At x = 1 cm and t = 1 sec
`y (1, 1) = 7.5 sin (0.005 xx 1 + 12 xx 1 pi/4) = 7.5 sin (12.005 + pi/4)` ....(i)
Now `theta = (12.005 + pi/4) "radian"`
`= 180/pi (12.005 + pi/4) "degree" = (12.005 xx 180)/(22/7) + 45 = 732.55^@`
`:. From (i), y(1,2) = 7.5 sin (732.55^@) = 7.5 sin (720 + 12.55^@)`
`= 7.5 sin 12.55^@ = 7.5 xx 0.2173 = 1.63 cm`
Velocity of oscillation `v = (dy)/(dt) (1,1) = d/dt[7.5 sin(0.005x + 12 + pi/4)]`
`= 7.5 xx 12 cos [0.005x + 12t + pi/4]`
At x = 1 cm, t = 1 sec
`v = 7.5 xx 12 cos (0.005 + 12 + pi/4) = 90 cos (732.35^@)`
= 90 cos (720 + 12.55)
`v = 90 cos (12.55^@) = 90 xx 0.9765 = 87.89 "cm/s"`
Comparing the given equation with the standard from `y(x,t)= t sin[pi/4 (vt + x) + phi_0]`
We get `r = 7.5 cm, (2piv)/lambda = 12 or 2 piv = 12 `
`v = 6/pi`
`(2pi)/lambda` = 0.005
`:. lambda = 2pi/0.005 = (2xx3.14)/0.005 = 1256 cm = 12.56 m`
Velocity of wave propagation, `v = vlambda = 6/pi xx 12.56 = 24 "m/s"`
We find that velocity at x = 1 cm, t = 1 sec is not equal tovelocity of waves propagation.
b) Now all point which are at a distance of `+- lambda +-2lambda, +- 3lambda` from x = 1 cm will have same tranverse displacement and velocity.As lambda = 12.56 m, therefore all points at distances `+- 12.6 m, +- 25.2 m, +- 37.8 m` from x = 1 cm will have same dispalcement and velocity as at x=1 point t =2 s, 5s and 11s
उत्तर २
For the stationary observer: 400 Hz; 0.875 m; 350 m/s
For the running observer: Not exactly identical
For the stationary observer:
Frequency of the sound produced by the whistle, ν = 400 Hz
Speed of sound = 340 m/s
Velocity of the wind, v = 10 m/s
As there is no relative motion between the source and the observer, the frequency of the sound heard by the observer will be the same as that produced by the source, i.e., 400 Hz.
The wind is blowing toward the observer. Hence, the effective speed of the sound increases by 10 units, i.e.,
Effective speed of the sound, ve = 340 + 10 = 350 m/s
The wavelength (λ) of the sound heard by the observer is given by the relation:
`lambda = V_e/V` = 350/400 = 0.875 m`
For the running observer:
Velocity of the observer, vo = 10 m/s
The observer is moving toward the source. As a result of the relative motions of the source and the observer, there is a change in frequency (v').
This is given by the relation:
`v' = ((v + v_0)/v)v`
`= ((340+ 10)/340) xx 400 = 411.76 "Hz"`
Since the air is still, the effective speed of sound = 340 + 0 = 340 m/s
The source is at rest. Hence, the wavelength of the sound will not change, i.e., λ remains 0.875 m.
Hence, the given two situations are not exactly identical.
APPEARS IN
संबंधित प्रश्न
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air increases with humidity.
A bat emits an ultrasonic sound of frequency 1000 kHz in the air. If the sound meets a water surface, what is the wavelength of the transmitted sound? The speed of sound in air is 340 m s–1 and in water 1486 m s–1.
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53 kHz. What is the speed of sound in steel?
A train, standing at the outer signal of a railway station blows a whistle of frequency 400 Hz in still air. (i) What is the frequency of the whistle for a platform observer when the train (a) approaches the platform with a speed of 10 m s–1, (b) recedes from the platform with a speed of 10 m s–1? (ii) What is the speed of sound in each case? The speed of sound in still air can be taken as 340 m s–1.
A SONAR system fixed in a submarine operates at a frequency 40.0 kHz. An enemy submarine moves towards the SONAR with a speed of 360 km h–1. What is the frequency of sound reflected by the submarine? Take the speed of sound in water to be 1450 m s–1.
A sine wave is travelling in a medium. The minimum distance between the two particles, always having same speed, is
Choose the correct option:
Which of the following equations represents a wave travelling along Y-axis?
Two strings A and B, made of same material, are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed `v_A` and on B with speed `v_B`. The ratio `v_A/v_B` is ______.
The equation of a wave travelling on a string stretched along the X-axis is given by
\[y = A e {}^- \left( \frac{x}{a} + \frac{t}{T} \right)^2 .\]
(a) Write the dimensions of A, a and T. (b) Find the wave speed. (c) In which direction is the wave travelling? (d) Where is the maximum of the pulse located at t = T? At t = 2 T?
A pulse travelling on a string is represented by the function \[y = \frac{a^2}{\left( x - \nu t \right)^2 + a^2},\] where a = 5 mm and ν = 20 cm-1. Sketch the shape of the string at t = 0, 1 s and 2 s. Take x = 0 in the middle of the string.
The displacement of the particle at x = 0 of a stretched string carrying a wave in the positive x-direction is given f(t) = A sin (t/T). The wave speed is v. Write the wave equation.
A wave propagates on a string in the positive x-direction at a velocity \[\nu\] \[t = t_0\] is given by \[g\left( x, t_0 \right) = A \sin \left( x/a \right)\]. Write the wave equation for a general time t.
A 200 Hz wave with amplitude 1 mm travels on a long string of linear mass density 6 g m−1 kept under a tension of 60 N. (a) Find the average power transmitted across a given point on the string. (b) Find the total energy associated with the wave in a 2⋅0 m long portion of the string.
Two waves, travelling in the same direction through the same region, have equal frequencies, wavelengths and amplitudes. If the amplitude of each wave is 4 mm and the phase difference between the waves is 90°, what is the resultant amplitude?
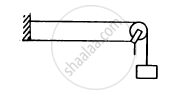
Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
An organ pipe of length 0.4 m is open at both ends. The speed of sound in the air is 340 m/s. The fundamental frequency is ______
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of `λ/2`.
A transverse harmonic wave on a string is described by y(x, t) = 3.0 sin (36t + 0.018x + π/4) where x and y are in cm and t is in s. The positive direction of x is from left to right.
- The wave is travelling from right to left.
- The speed of the wave is 20 m/s.
- Frequency of the wave is 5.7 Hz.
- The least distance between two successive crests in the wave is 2.5 cm.
At what temperatures (in °C) will the speed of sound in air be 3 times its value at O°C?
If c is r.m.s. speed of molecules in a gas and v is the speed of sound waves in the gas, show that c/v is constant and independent of temperature for all diatomic gases.
