Advertisements
Advertisements
प्रश्न
Show that the particle speed can never be equal to the wave speed in a sine wave if the amplitude is less than wavelength divided by 2π.
उत्तर
Equation of the wave is given by
\[y = A\sin\left( \omega t - kx \right)\]
where
A is the amplitude
ω is the angular frequency
k is the wave number
Velocity of wave, \[y = A\sin\left( \omega t - kx \right)\]
Velocity of particle, \[v_p = \frac{dy}{dt} = A\omega \cos\left( \omega t - kx \right)\]
Max velocity of particle,
\[v_{p_\max} = A\omega\]
As given
\[A < \frac{\lambda}{2\pi}\]
\[v_{p_\max} = \frac{\lambda\omega}{2\pi}\]
\[ v_{p_\max} < \frac{\omega}{k} \left[ \because \frac{2\pi}{\lambda} = k \right]\]
APPEARS IN
संबंधित प्रश्न
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air increases with humidity.
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45 Hz. The mass of the wire is 3.5 × 10–2 kg and its linear mass density is 4.0 × 10–2 kg m–1. What is (a) the speed of a transverse wave on the string, and (b) the tension in the string?
Show that for a wave travelling on a string
\[\frac{y_{max}}{\nu_{max}} = \frac{\nu_{max}}{\alpha_{max}},\]
where the symbols have usual meanings. Can we use componendo and dividendo taught in algebra to write
\[\frac{y_{max} + \nu_{max}}{\nu_{max} - \nu_{max}} = \frac{\nu_{max} + \alpha_{max}}{\nu_{max} - \alpha_{max}}?\]
A sine wave is travelling in a medium. The minimum distance between the two particles, always having same speed, is
A sine wave is travelling in a medium. A particular particle has zero displacement at a certain instant. The particle closest to it having zero displacement is at a distance
Two wave pulses travel in opposite directions on a string and approach each other. The shape of one pulse is inverted with respect to the other.
Two sine waves travel in the same direction in a medium. The amplitude of each wave is A and the phase difference between the two waves is 120°. The resultant amplitude will be
The displacement of the particle at x = 0 of a stretched string carrying a wave in the positive x-direction is given f(t) = A sin (t/T). The wave speed is v. Write the wave equation.
The equation of a wave travelling on a string is \[y = \left( 0 \cdot 10 \text{ mm } \right) \sin\left[ \left( 31 \cdot 4 m^{- 1} \right)x + \left( 314 s^{- 1} \right)t \right]\]
(a) In which direction does the wave travel? (b) Find the wave speed, the wavelength and the frequency of the wave. (c) What is the maximum displacement and the maximum speed of a portion of the string?
A wave travelling on a string at a speed of 10 m s−1 causes each particle of the string to oscillate with a time period of 20 ms. (a) What is the wavelength of the wave? (b) If the displacement of a particle of 1⋅5 mm at a certain instant, what will be the displacement of a particle 10 cm away from it at the same instant?
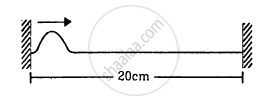
A string of length 20 cm and linear mass density 0⋅40 g cm−1 is fixed at both ends and is kept under a tension of 16 N. A wave pulse is produced at t = 0 near an ends as shown in the figure, which travels towards the other end. (a) When will the string have the shape shown in the figure again? (b) Sketch the shape of the string at a time half of that found in part (a).
The equation for the vibration of a string, fixed at both ends vibrating in its third harmonic, is given by
\[y = \left( 0 \cdot 4 cm \right) \sin\left[ \left( 0 \cdot 314 {cm}^{- 1} \right) x \right] \cos \left[ \left( 600\pi s^{- 1} \right) t \right]\]
(a) What is the frequency of vibration? (b) What are the positions of the nodes? (c) What is the length of the string? (d) What is the wavelength and the speed of two travelling waves that can interfere to give this vibration?
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of 4 m.
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of `λ/2`.
Speed of sound wave in air ______.
A sound wave is passing through air column in the form of compression and rarefaction. In consecutive compressions and rarefactions ______.
A string of mass 2.5 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, the disturbance will reach the other end in ______.
Speed of sound waves in a fluid depends upon ______.
- directty on density of the medium.
- square of Bulk modulus of the medium.
- inversly on the square root of density.
- directly on the square root of bulk modulus of the medium.
If c is r.m.s. speed of molecules in a gas and v is the speed of sound waves in the gas, show that c/v is constant and independent of temperature for all diatomic gases.
Two perfectly identical wires kept under tension are in unison. When the tension in the wire is increased by 1% then on sounding them together 3 beats are heard in 2 seconds. What is the frequency of each wire?
