Advertisements
Advertisements
प्रश्न
A string of length 20 cm and linear mass density 0⋅40 g cm−1 is fixed at both ends and is kept under a tension of 16 N. A wave pulse is produced at t = 0 near an ends as shown in the figure, which travels towards the other end. (a) When will the string have the shape shown in the figure again? (b) Sketch the shape of the string at a time half of that found in part (a).
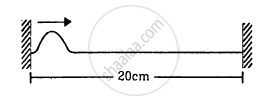
उत्तर
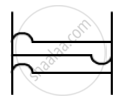
Given,
Length of the string = 20 cm
Linear mass density of the string = 0.40 g cm−1
Applied tension = 16 N = \[16 \times {10}^5 dyn\]
Velocity of the wave:
\[\nu = \sqrt{\left( \frac{T}{m} \right)}\]
\[ = \sqrt{\frac{\left( 16 \times {10}^5 \right)}{0 . 4}}\]
\[ = 2000 \text{ cm }/s\]
∴ Time taken to reach the other end
\[= \frac{20}{2000} = 0 . 01 s\]
Time taken to see the pulse again in the original position
\[= 0 . 01 \times 2 = 0 . 02 s\]
(b) At t = 0.01 s, there will be a trough at the right end as it is reflected.
APPEARS IN
संबंधित प्रश्न
A stone dropped from the top of a tower of height 300 m high splashes into the water of a pond near the base of the tower. When is the splash heard at the top given that the speed of sound in air is 340 m s–1? (g= 9.8 m s–2)
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air increases with humidity.
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45 Hz. The mass of the wire is 3.5 × 10–2 kg and its linear mass density is 4.0 × 10–2 kg m–1. What is (a) the speed of a transverse wave on the string, and (b) the tension in the string?
A metre-long tube open at one end, with a movable piston at the other end, shows resonance with a fixed frequency source (a tuning fork of frequency 340 Hz) when the tube length is 25.5 cm or 79.3 cm. Estimate the speed of sound in air at the temperature of the experiment. The edge effects may be neglected.
A train, standing in a station-yard, blows a whistle of frequency 400 Hz in still air. The wind starts blowing in the direction from the yard to the station with at a speed of 10 m s–1. What are the frequency, wavelength, and speed of sound for an observer standing on the station’s platform? Is the situation exactly identical to the case when the air is still and the observer runs towards the yard at a speed of 10 m s–1? The speed of sound in still air can be taken as 340 m s–1.
Two strings A and B, made of same material, are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed `v_A` and on B with speed `v_B`. The ratio `v_A/v_B` is ______.
Two wave pulses travel in opposite directions on a string and approach each other. The shape of one pulse is inverted with respect to the other.
A sonometer wire supports a 4 kg load and vibrates in fundamental mode with a tuning fork of frequency 416. Hz. The length of the wire between the bridges is now doubled. In order to maintain fundamental mode, the load should be changed to
A wave pulse is travelling on a string with a speed \[\nu\] towards the positive X-axis. The shape of the string at t = 0 is given by g(x) = Asin(x/a), where A and a are constants. (a) What are the dimensions of A and a ? (b) Write the equation of the wave for a general time t, if the wave speed is \[\nu\].
A wave propagates on a string in the positive x-direction at a velocity \[\nu\] \[t = t_0\] is given by \[g\left( x, t_0 \right) = A \sin \left( x/a \right)\]. Write the wave equation for a general time t.
Two waves, travelling in the same direction through the same region, have equal frequencies, wavelengths and amplitudes. If the amplitude of each wave is 4 mm and the phase difference between the waves is 90°, what is the resultant amplitude?
A wire of length 2⋅00 m is stretched to a tension of 160 N. If the fundamental frequency of vibration is 100 Hz, find its linear mass density.
The equation for the vibration of a string, fixed at both ends vibrating in its third harmonic, is given by
\[y = \left( 0 \cdot 4 cm \right) \sin\left[ \left( 0 \cdot 314 {cm}^{- 1} \right) x \right] \cos \left[ \left( 600\pi s^{- 1} \right) t \right]\]
(a) What is the frequency of vibration? (b) What are the positions of the nodes? (c) What is the length of the string? (d) What is the wavelength and the speed of two travelling waves that can interfere to give this vibration?
A 40 cm wire having a mass of 3⋅2 g is stretched between two fixed supports 40⋅05 cm apart. In its fundamental mode, the wire vibrates at 220 Hz. If the area of cross section of the wire is 1⋅0 mm2, find its Young modulus.
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of 0.5 m.
Sound waves of wavelength λ travelling in a medium with a speed of v m/s enter into another medium where its speed is 2v m/s. Wavelength of sound waves in the second medium is ______.
A string of mass 2.5 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, the disturbance will reach the other end in ______.
If c is r.m.s. speed of molecules in a gas and v is the speed of sound waves in the gas, show that c/v is constant and independent of temperature for all diatomic gases.
