Advertisements
Advertisements
प्रश्न
A 40 cm wire having a mass of 3⋅2 g is stretched between two fixed supports 40⋅05 cm apart. In its fundamental mode, the wire vibrates at 220 Hz. If the area of cross section of the wire is 1⋅0 mm2, find its Young modulus.
उत्तर
Given:
Length of the wire (L) = 40 cm = 0.40 m
Mass of the wire = 3.2 g = 0.003 kg
Distance between the two fixed supports of the wire = 40.05 cm
Fundamental mode frequency = 220 Hz
Therefore, linear mass density of the wire (m) is given by:
\[m = \frac{0 . 0032}{0 . 4} = 8 \times {10}^{- 3} kg/m\]
\[\text{ Change in length, } ∆ L = 40 . 05 - 40 = 0 . 05 cm\]
\[= 0 . 05 \times {10}^{- 2} m\]
\[Strain = \frac{∆ L}{L} = \frac{0 . 05 \times {10}^{- 2}}{0 . 4}\]
\[ = 0 . 125 \times {10}^{- 2} \]
\[ f_0 = \frac{1}{2L}\sqrt{\frac{T}{m}}\]
\[ = \frac{1}{2 \times \left( 0 . 4005 \right)} \sqrt{\frac{T}{8 \times {10}^{- 3}}}\]
\[\Rightarrow 220 \times 220 = \left[ \frac{1}{\left( 0 . 801 \right)^2} \right] \times T \times \left( \frac{{10}^3}{8} \right)\]
\[ \Rightarrow T \times 1000 = 220 \times 220 \times 0 . 641 \times 0 . 8\]
\[ \Rightarrow T = 248 . 19 N\]
\[Stress = \frac{Tension}{Area} = \frac{248 . 19}{1 {mm}^2} = \frac{248 . 19}{{10}^{- 6}}\]
\[ \Rightarrow Stress = 248 . 19 \times {10}^6 \]
\[\text{ Young's modulus, } Y = \frac{stress}{strain}\]
\[ = \frac{248 . 19 \times {10}^6}{0 . 125 \times {10}^{- 2}}\]
\[ \Rightarrow Y = 19852 \times {10}^8 \]
\[ = 1 . 985 \times {10}^{11} N/ m^2\]
Hence, the required Young's modulus of the wire is
\[1 . 985 \times {10}^{11} N/ m^2\]
APPEARS IN
संबंधित प्रश्न
A steel wire has a length of 12.0 m and a mass of 2.10 kg. What should be the tension in the wire so that speed of a transverse wave on the wire equals the speed of sound in dry air at 20 °C = 343 m s–1.
You have learnt that a travelling wave in one dimension is represented by a function y= f (x, t)where x and t must appear in the combination x – v t or x + v t, i.e. y = f (x ± v t). Is the converse true? Examine if the following functions for y can possibly represent a travelling wave:
(a) `(x – vt )^2`
(b) `log [(x + vt)/x_0]`
(c) `1/(x + vt)`
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of `(3λ)/4`.
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53 kHz. What is the speed of sound in steel?
The radio and TV programmes, telecast at the studio, reach our antenna by wave motion. Is it a mechanical wave or nonmechanical?
A sine wave is travelling in a medium. The minimum distance between the two particles, always having same speed, is
A sine wave is travelling in a medium. A particular particle has zero displacement at a certain instant. The particle closest to it having zero displacement is at a distance
Two wave pulses travel in opposite directions on a string and approach each other. The shape of one pulse is inverted with respect to the other.
A sonometer wire of length l vibrates in fundamental mode when excited by a tuning fork of frequency 416. Hz. If the length is doubled keeping other things same, the string will ______.
A sonometer wire supports a 4 kg load and vibrates in fundamental mode with a tuning fork of frequency 416. Hz. The length of the wire between the bridges is now doubled. In order to maintain fundamental mode, the load should be changed to
A pulse travelling on a string is represented by the function \[y = \frac{a^2}{\left( x - \nu t \right)^2 + a^2},\] where a = 5 mm and ν = 20 cm-1. Sketch the shape of the string at t = 0, 1 s and 2 s. Take x = 0 in the middle of the string.
A wave pulse is travelling on a string with a speed \[\nu\] towards the positive X-axis. The shape of the string at t = 0 is given by g(x) = Asin(x/a), where A and a are constants. (a) What are the dimensions of A and a ? (b) Write the equation of the wave for a general time t, if the wave speed is \[\nu\].
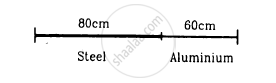
Figure shows an aluminium wire of length 60 cm joined to a steel wire of length 80 cm and stretched between two fixed supports. The tension produced is 40 N. The cross-sectional area of the steel wire is 1⋅0 mm2 and that of the aluminium wire is 3⋅0 mm2. What could be the minimum frequency of a tuning fork which can produce standing waves in the system with the joint as a node? The density of aluminium is 2⋅6 g cm−3 and that of steel is 7⋅8 g cm−3.
A man standing unsymmetrical position between two mountains and fires a gun. He hears the first echo after 1.5 s and the second echo after 2.5 s. If the speed of sound in air is 340 m/s, then the distance between the mountains will be ______
What is the interference of sound waves?
A string 1 m long is fixed at one end. The other end is moved up and down with a frequency of 20 Hz. Due to this, a stationary wave with four complete loops gets produced on the string. Find the speed of the progressive wave which produces the stationary wave.
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of 0.5 m.
A steel wire has a length of 12 m and a mass of 2.10 kg. What will be the speed of a transverse wave on this wire when a tension of 2.06 × 104N is applied?
Two perfectly identical wires kept under tension are in unison. When the tension in the wire is increased by 1% then on sounding them together 3 beats are heard in 2 seconds. What is the frequency of each wire?
