Question

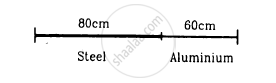
Figure shows an aluminium wire of length 60 cm joined to a steel wire of length 80 cm and stretched between two fixed supports. The tension produced is 40 N. The cross-sectional area of the steel wire is 1⋅0 mm² and that of the aluminium wire is 3⋅0 mm². What could be the minimum frequency of a tuning fork which can produce standing waves in the system with the joint as a node? The density of aluminium is 2⋅6 g cm⁻³ and that of steel is 7⋅8 g cm⁻³.

Answer 1

Given:
Length of the aluminium wire (L_a)= 60 cm = 0.60 m
Length of the steel wire (L_s)= 80 cm = 0.80 m
Tension produced (T) = 40 N
Area of cross-section of the aluminium wire (A_a)  = 1.0 mm²
Area of cross-section of the steel wire (A_s) = 3.0 mm²
Density of aluminium (ρ_a) = 2⋅6 g cm⁻³
Density of steel  (ρ_s) = 7⋅8 g cm⁻³  

\[\text{ Mass  per  unit  length  of  the  steel,    m_s }    =  \rho_s  \times  A_s \] 

\[   = 7 . 8 \times  {10}^{- 2}   gm/cm\] 

\[  = 7 . 8 \times  {10}^{- 3}   kg/m\] 

\[\text{ Mass  per  unit  length  of  the  aluminium,    m_A  }=  \rho_A  A_A \] 

\[   = 2 . 6 \times  {10}^{- 2}  \times 3  gm/cm\] 

\[ = 7 . 8 \times  {10}^{- 2}   gm/cm\] 

\[ = 7 . 8 \times  {10}^{- 3}   kg/m\]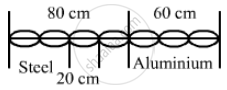

A node is always placed at the joint. Since aluminium and steel rod has same mass per unit length, the velocity of wave (v) in both of them is same.
Let v be the velocity of wave.

\[\Rightarrow v = \left( \frac{T}{m} \right)\] 

\[ =  \sqrt{\left\{ \frac{40}{7 . 8 \times {10}^{- 3}} \right\}}^- \] 

\[  = \sqrt{\left( \frac{4 \times {10}^4}{7 . 8} \right)}\] 

\[ \Rightarrow v = 71 . 6  m/s\]
For minimum frequency, there would be maximum wavelength.
For maximum wavelength, minimum number of loops are to be produced.
∴ Maximum distance of a loop = 20 cm

\[\Rightarrow   \text{ Wavelength, }   \lambda = 2 \times 20 = 40  cm\] 

\[\text{ Or }  \lambda = 0 . 4  m\] 

\[ \therefore Frequency,   f = \frac{v}{\lambda} = \frac{71 . 6}{0 . 4} = 180  Hz\]