Advertisements
Advertisements
प्रश्न
Given below are some functions of x and t to represent the displacement of an elastic wave.
- y = 5 cos (4x) sin (20t)
- y = 4 sin (5x – t/2) + 3 cos (5x – t/2)
- y = 10 cos [(252 – 250) πt] cos [(252 + 250)πt]
- y = 100 cos (100πt + 0.5x)
State which of these represent
- a travelling wave along –x direction
- a stationary wave
- beats
- a travelling wave along +x direction.
Given reasons for your answers.
उत्तर
- The equation y = 100 cos(100πt + 0.5x) is representing a travelling wave along the x-direction.
- The equation y = 5 cos(4x) sin(20t) represents a stationary wave because it contains sin, cos terms i.e., the combination of two progressive waves
- As the equation y = 10 cos[(252 – 250)πt] – cos[(252 + 250)πt] involving the sum and difference of two nearby frequencies 252 and 250 this equation represents beats formation.
- As the equation, y = 4 sin(5x – t/2) + 3 cos(5x – t/2) involves a negative sign with x, have if represents a travelling wave along the x-direction.
APPEARS IN
संबंधित प्रश्न
(i) For the wave on a string described in Exercise 15.11, do all the points on the string oscillate with the same (a) frequency, (b) phase, (c) amplitude? Explain your answers. (ii) What is the amplitude of a point 0.375 m away from one end?
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45 Hz. The mass of the wire is 3.5 × 10–2 kg and its linear mass density is 4.0 × 10–2 kg m–1. What is (a) the speed of a transverse wave on the string, and (b) the tension in the string?
Show that for a wave travelling on a string
\[\frac{y_{max}}{\nu_{max}} = \frac{\nu_{max}}{\alpha_{max}},\]
where the symbols have usual meanings. Can we use componendo and dividendo taught in algebra to write
\[\frac{y_{max} + \nu_{max}}{\nu_{max} - \nu_{max}} = \frac{\nu_{max} + \alpha_{max}}{\nu_{max} - \alpha_{max}}?\]
Two waves of equal amplitude A, and equal frequency travel in the same direction in a medium. The amplitude of the resultant wave is
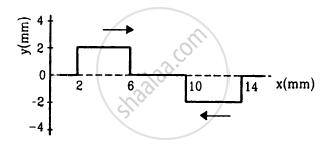
Following figure shows two wave pulses at t = 0 travelling on a string in opposite directions with the same wave speed 50 cm s−1. Sketch the shape of the string at t = 4 ms, 6 ms, 8 ms, and 12 ms.
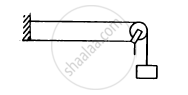
Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
An organ pipe of length 0.4 m is open at both ends. The speed of sound in the air is 340 m/s. The fundamental frequency is ______
A string 1 m long is fixed at one end. The other end is moved up and down with a frequency of 20 Hz. Due to this, a stationary wave with four complete loops gets produced on the string. Find the speed of the progressive wave which produces the stationary wave.
At what temperatures (in °C) will the speed of sound in air be 3 times its value at O°C?
The displacement y of a particle in a medium can be expressed as, y = `10^-6sin(100t + 20x + pi/4)` m where t is in second and x in meter. The speed of the wave is ______.
