Advertisements
Advertisements
प्रश्न
A uniform horizontal rod of length 40 cm and mass 1⋅2 kg is supported by two identical wires as shown in figure. Where should a mass of 4⋅8 kg be placed on the rod so that the same tuning fork may excite the wire on left into its fundamental vibrations and that on right into its first overtone? Take g = 10 m s−2.
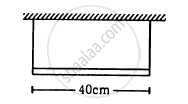
उत्तर
Given:
Length of the rod (L) = 40 cm = 0.40 m
Mass of the rod (m) = 1.2 kg
Let the mass of 4.8 kg be placed at x distance from the left.
As per the question, frequency on the left side = f0
Frequency on the right side = 2f0
Let tension be T1 and T2 on the left and the right side, respectively.
\[\therefore \frac{1}{2L}\sqrt{\frac{T_1}{m}} = \frac{2}{2L}\sqrt{\frac{T_2}{m}}\]
\[ \Rightarrow \sqrt{\frac{T_1}{T_2}} = 2\]
\[ \Rightarrow \frac{T_1}{T_2} = 4 . . . (1)\]
From the free body diagram: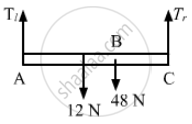
\[T_1 + T_2 = 48 + 12 = 60 N\]
\[ \Rightarrow 4 T_2 + T_2 = 5 T_2 = 60 N \left[ \text{ using equation } \left( 1 \right) \right]\]
\[ \therefore T_2 = 12 N\]
\[\text{ and } T_1 = 48 N\]
Now, taking moment about point A: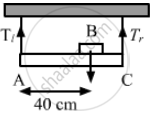
\[T_2 \times \left( 0 . 4 \right) = 48x + 12 \times 0 . 2\]
\[ \Rightarrow 4 . 8 = 48x - 2 . 4\]
\[ \Rightarrow 4 . 8x = 2 . 4\]
\[ \Rightarrow x = \frac{2 . 4}{4 . 8} = \frac{1}{20} m = 5 \text{ cm }\]
Therefore, the mass should be placed at a distance of 5 cm from the left end.
APPEARS IN
संबंधित प्रश्न
A wave is represented by an equation \[y = c_1 \sin \left( c_2 x + c_3 t \right)\] In which direction is the wave going? Assume that \[c_1 , c_2\] \[c_3\] are all positive.
The voice of a person, who has inhaled helium, has a remarkably high pitch. Explain on the basis of resonant vibration of vocal cord filled with air and with helium.
Two tuning forks vibrate with the same amplitude but the frequency of the first is double the frequency of the second. Which fork produces more intense sound in air?
When we clap our hands, the sound produced is best described by Here p denotes the change in pressure from the equilibrium value.
A tuning fork sends sound waves in air. If the temperature of the air increases, which of the following parameters will change?
Two sound waves move in the same direction in the same medium. The pressure amplitudes of the waves are equal but the wavelength of the first wave is double the second. Let the average power transmitted across a cross section by the first wave be P1 and that by the second wave be P2. Then
A tuning fork of frequency 512 Hz is vibrated with a sonometer wire and 6 beats per second are heard. The beat frequency reduces if the tension in the string is slightly increased. The original frequency of vibration of the string is
An electrically maintained tuning fork vibrates with constant frequency and constant amplitude. If the temperature of the surrounding air increases but pressure remains constant, the produced will have
(a) larger wavelength
(b) larger frequency
(c) larger velocity
(d) larger time period.
A source of sound moves towards an observer.
A listener is at rest with respect to the source of sound. A wind starts blowing along the line joining the source and the observer. Which of the following quantities do not change?
(a) Frequency
(b) Velocity of sound
(c) Wavelength
(d) Time period
If the intensity of sound is doubled, by how many decibels does the sound level increase?
A string, fixed at both ends, vibrates in a resonant mode with a separation of 2⋅0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1⋅6 cm. Find the length of the string.
A string of length L fixed at both ends vibrates in its fundamental mode at a frequency ν and a maximum amplitude A. (a)
- Find the wavelength and the wave number k.
- Take the origin at one end of the string and the X-axis along the string. Take the Y-axis along the direction of the displacement. Take t = 0 at the instant when the middle point of the string passes through its mean position and is going towards the positive y-direction. Write the equation describing the standing wave.
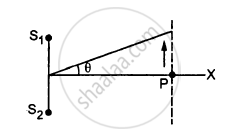
Two speakers S1 and S2, driven by the same amplifier, are placed at y = 1.0 m and y = −1.0 m(See figure). The speakers vibrate in phase at 600 Hz. A man stands at a point on the X-axis at a very large distance from the origin and starts moving parallel to the Y-axis. The speed of sound in air is 330 m s−1. (a) At what angle θ will the intensity of sound drop to a minimum for the first time? (b) At what angle will he hear a maximum of sound intensity for the first time? (c) If he continues to walk along the line, how many more can he hear?
Three sources of sound S1, S2 and S3 of equal intensity are placed in a straight line with S1S2 = S2S3. At a point P, far away from the sources, the wave coming from S2 is 120° ahead in phase of that from S1. Also, the wave coming from S3 is 120° ahead of that from S2. What would be the resultant intensity of sound at P?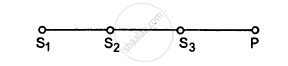
In a standing wave pattern in a vibrating air column, nodes are formed at a distance of 4.0 cm. If the speed of sound in air is 328 m s−1, what is the frequency of the source?
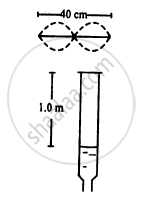
Consider the situation shown in the figure.The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 340 m s−1, find the tension in the wire.
The fundamental frequency of a closed pipe is 293 Hz when the air in it is a temperature of 20°C. What will be its fundamental frequency when the temperature changes to 22°C?
Show that if the room temperature changes by a small amount from T to T + ∆T, the fundamental frequency of an organ pipe changes from v to v + ∆v, where \[\frac{∆ v}{v} = \frac{1}{2}\frac{∆ T}{T} .\]
