Advertisements
Advertisements
प्रश्न
If the intensity of sound is doubled, by how many decibels does the sound level increase?
उत्तर
Let the intensity of the sound be I and \[\beta_1\] be the sound level. If the intensity of the sound is doubled, then its sound level becomes 2I.
Sound level \[\beta_1\] is given by ,\[\beta_1 = 10 \log_{10} \frac{I}{I_0}\],
where I0 is the constant reference intensity.
When the intensity doubles, the sound level is given by:
\[\beta_2 = 10 \log_{10} \frac{2I}{I_0}\].
According to the question,
\[ \beta_2 - \beta_1 = 10 \log\left( \frac{2I}{I} \right)\]
\[ = 10 \times 0 . 3010 = 3 \text{ dB }\]
The sound level is increased by 3 dB.
APPEARS IN
संबंधित प्रश्न
What is the smallest positive phase constant which is equivalent to 7⋅5 π?
A string clamped at both ends vibrates in its fundamental mode. Is there any position (except the ends) on the string which can be touched without disturbing the motion? What if the string vibrates in its first overtone?
The equation \[y = A \sin^2 \left( kx - \omega t \right)\]
represents a wave motion with
Can you hear your own words if you are standing in a perfect vacuum? Can you hear your friend in the same conditions?
Two tuning forks vibrate with the same amplitude but the frequency of the first is double the frequency of the second. Which fork produces more intense sound in air?
When we clap our hands, the sound produced is best described by Here p denotes the change in pressure from the equilibrium value.
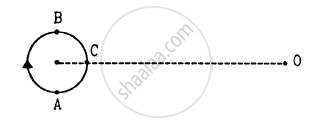
A small source of sounds moves on a circle as shown in figure and an observer is sitting at O. Let \[v_1, v_2, v_3\] be the frequencies heard when the source is at A, B and C respectively.
The fundamental frequency of a vibrating organ pipe is 200 Hz.
(a) The first overtone is 400 Hz.
(b) The first overtone may be 400 Hz.
(c) The first overtone may be 600 Hz.
(d) 600 Hz is an overtone.
Find the minimum and maximum wavelengths of sound in water that is in the audible range (20−20000 Hz) for an average human ear. Speed of sound in water = 1450 m s−1.
The sound level at a point 5.0 m away from a point source is 40 dB. What will be the level at a point 50 m away from the source?
The noise level in a classroom in absence of the teacher is 50 dB when 50 students are present. Assuming that on the average each student output same sound energy per second, what will be the noise level if the number of students is increased to 100?
A string of length L fixed at both ends vibrates in its fundamental mode at a frequency ν and a maximum amplitude A. (a)
- Find the wavelength and the wave number k.
- Take the origin at one end of the string and the X-axis along the string. Take the Y-axis along the direction of the displacement. Take t = 0 at the instant when the middle point of the string passes through its mean position and is going towards the positive y-direction. Write the equation describing the standing wave.
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The sound is detected by moving a detector on the screen ∑ at a distance D(>>λ) from the slit S1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.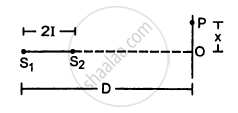
A tuning fork produces 4 beats per second with another tuning fork of frequency 256 Hz. The first one is now loaded with a little wax and the beat frequency is found to increase to 6 per second. What was the original frequency of the tuning fork?
Show that if the room temperature changes by a small amount from T to T + ∆T, the fundamental frequency of an organ pipe changes from v to v + ∆v, where \[\frac{∆ v}{v} = \frac{1}{2}\frac{∆ T}{T} .\]
A cylindrical tube, open at both ends, has a fundamental frequency v. The tube is dipped vertically in water so that half of its length is inside the water. The new fundamental frequency is
A sound source, fixed at the origin, is continuously emitting sound at a frequency of 660 Hz. The sound travels in air at a speed of 330 m s−1. A listener is moving along the lien x= 336 m at a constant speed of 26 m s−1. Find the frequency of the sound as observed by the listener when he is (a) at y = − 140 m, (b) at y = 0 and (c) at y = 140 m.
A car moves with a speed of 54 km h−1 towards a cliff. The horn of the car emits sound of frequency 400 Hz at a speed of 335 m s−1. (a) Find the wavelength of the sound emitted by the horn in front of the car. (b) Find the wavelength of the wave reflected from the cliff. (c) What frequency does a person sitting in the car hear for the reflected sound wave? (d) How many beats does he hear in 10 seconds between the sound coming directly from the horn and that coming after the reflection?
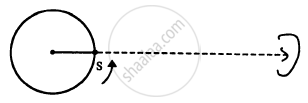
A small source of sound S of frequency 500 Hz is attached to the end of a light string and is whirled in a vertical circle of radius 1.6 m. The string just remains tight when the source is at the highest point. (a) An observer is located in the same vertical plane at a large distance and at the same height as the centre of the circle. The speed of sound in air = 330 m s−1 and g = 10 m s−2. Find the maximum frequency heard by the observer. (b) An observer is situated at a large distance vertically above the centre of the circle. Find the frequency heard by the observer corresponding to the sound emitted by the source when it is at the same height as the centre.
For the propagation of longitudinal waves, the medium must have
- elasticity
- mass
- inertia
- force of cohesion
