Advertisements
Advertisements
प्रश्न
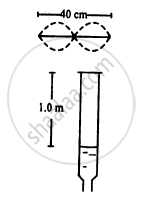
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The sound is detected by moving a detector on the screen ∑ at a distance D(>>λ) from the slit S1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.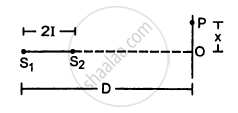
उत्तर
Given:
S1& S2 are in the same phase. At O, there will be maximum intensity.
There will be maximum intensity at P.
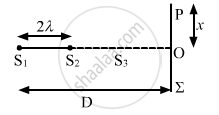
\[∆ S_1 PO\] and \[∆ S_2 PO\] are right-angled triangles.
So,
\[\left( S_1 P \right)^2 - \left( S_2 P \right)^2 \]
\[ = \left[ D^2 + x^2 \right] - \left[ \left( D - 2\lambda \right)^2 + x^2 \right]^2 \]
\[ = 4\lambda D + 4 \lambda^2 = 4\lambda D\]
\[( \lambda^2 \text { is small and can be neglected })\]
\[ \Rightarrow \left( S_1 P + S_2 P \right)\left( S_1 P - S_2 P \right) = 4\lambda D\]
\[ \Rightarrow \left( S_1 P - S_2 P \right) = \frac{4\lambda D}{\left( S_1 P + S_2 P \right)}\]
\[ \Rightarrow S_1 P - S_2 P = \frac{4\lambda D}{2\sqrt{x^2 + D^2}}\]
For constructive interference, path difference = n \[\lambda\]
So,
\[\Rightarrow S_1 P - S_2 P = \frac{4\lambda D}{2\sqrt{x^2 + D^2}} = n\lambda\]
\[ \Rightarrow \frac{2D}{\sqrt{x^2 + D^2}} = n\]
\[ \Rightarrow n^2 ( x^2 + D^2 ) = 4 D^2 \]
\[ \Rightarrow n^2 x^2 + n^2 D^2 = 4 D^2 \]
\[ \Rightarrow n^2 x^2 = 4 D^2 - n^2 D^2 \]
\[ \Rightarrow n^2 x^2 = D^2 \left( 4 - n^2 \right)\]
\[ \Rightarrow x = \frac{D}{n}\sqrt{4 - n^2}\]
\[\text { When n = 1 }, \]
\[x = \sqrt{3}D (\text { 1st order }) . \]
\[\text { When n } = 2, \]
\[x = 0 \ (\text { 2nd order }) . \]
So, when x = \[\sqrt{3}D\] , the intensity at P is equal to the intensity at O.
APPEARS IN
संबंधित प्रश्न
Explain what is Doppler effect in sound
Can you hear your own words if you are standing in a perfect vacuum? Can you hear your friend in the same conditions?
A tuning fork sends sound waves in air. If the temperature of the air increases, which of the following parameters will change?
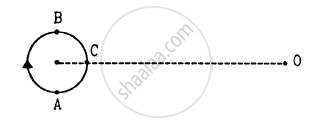
A small source of sounds moves on a circle as shown in figure and an observer is sitting at O. Let \[v_1, v_2, v_3\] be the frequencies heard when the source is at A, B and C respectively.
A steel tube of length 1.00 m is struck at one end. A person with his ear closed to the other end hears the sound of the blow twice, one travelling through the body of the tube and the other through the air in the tube. Find the time gap between the two hearings. Use the table in the text for speeds of sound in various substances.
A person can hear sound waves in the frequency range 20 Hz to 20 kHz. Find the minimum and the maximum wavelengths of sound that is audible to the person. The speed of sound is 360 m s−1.
Sound waves from a loudspeaker spread nearly uniformly in all directions if the wavelength of the sound is much larger than the diameter of the loudspeaker. (a)Calculate the frequency for which the wavelength of sound in air is ten times the diameter of the speaker if the diameter is 20 cm. (b) Sound is essentially transmitted in the forward direction if the wavelength is much shorter than the diameter of the speaker. Calculate the frequency at which the wavelength of the sound is one tenth of the diameter of the speaker described above. Take the speed of sound to be 340 m/s.
The equation of a travelling sound wave is y = 6.0 sin (600 t − 1.8 x) where y is measured in 10−5 m, t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed.
At what temperature will the speed of sound be double of its value at 0°C?
A sources of sound operates at 2.0 kHz, 20 W emitting sound uniformly in all directions. The speed of sound in air is 340 m s−1 and the density of air is 1.2 kg m −3. (a) What is the intensity at a distance of 6.0 m from the source? (b) What will be the pressure amplitude at this point? (c) What will be the displacement amplitude at this point?
A string, fixed at both ends, vibrates in a resonant mode with a separation of 2⋅0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1⋅6 cm. Find the length of the string.
A particular guitar wire is 30⋅0 cm long and vibrates at a frequency of 196 Hz when no finger is placed on it. The next higher notes on the scale are 220 Hz, 247 Hz, 262 Hz and 294 Hz. How far from the end of the string must the finger be placed to play these notes?
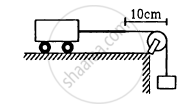
A heavy string is tied at one end to a movable support and to a light thread at the other end as shown in following figure. The thread goes over a fixed pulley and supports a weight to produce a tension. The lowest frequency with which the heavy string resonates is 120 Hz. If the movable support is pushed to the right by 10 cm so that the joint is placed on the pulley, what will be the minimum frequency at which the heavy string can resonate?
The first overtone frequency of a closed organ pipe P1 is equal to the fundamental frequency of a open organ pipe P2. If the length of the pipe P1 is 30 cm, what will be the length of P2?
Consider the situation shown in the figure.The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 340 m s−1, find the tension in the wire.
A traffic policeman standing on a road sounds a whistle emitting the main frequency of 2.00 kHz. What could be the apparent frequency heard by a scooter-driver approaching the policeman at a speed of 36.0 km h−1? Speed of sound in air = 340 m s−1.
A boy riding on his bike is going towards east at a speed of 4√2 m s−1. At a certain point he produces a sound pulse of frequency 1650 Hz that travels in air at a speed of 334 m s−1. A second boy stands on the ground 45° south of east from his. Find the frequency of the pulse as received by the second boy.
A train running at 108 km h−1 towards east whistles at a dominant frequency of 500 Hz. Speed of sound in air is 340 m/s. What frequency will a passenger sitting near the open window hear? (b) What frequency will a person standing near the track hear whom the train has just passed? (c) A wind starts blowing towards east at a speed of 36 km h−1. Calculate the frequencies heard by the passenger in the train and by the person standing near the track.
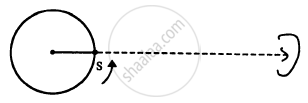
A small source of sound S of frequency 500 Hz is attached to the end of a light string and is whirled in a vertical circle of radius 1.6 m. The string just remains tight when the source is at the highest point. (a) An observer is located in the same vertical plane at a large distance and at the same height as the centre of the circle. The speed of sound in air = 330 m s−1 and g = 10 m s−2. Find the maximum frequency heard by the observer. (b) An observer is situated at a large distance vertically above the centre of the circle. Find the frequency heard by the observer corresponding to the sound emitted by the source when it is at the same height as the centre.
In an experiment to determine the velocity of sound in air at room temperature using a resonance tube, the first resonance is observed when the air column has a length of 20.0 cm for a tuning fork of frequency 400 Hz is used. The velocity of the sound at room temperature is 336 ms-1. The third resonance is observed when the air column has a length of ______ cm.
