Advertisements
Advertisements
प्रश्न
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The sound is detected by moving a detector on the screen ∑ at a distance D(>>λ) from the slit S1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.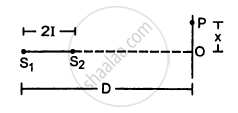
उत्तर
Given:
S1& S2 are in the same phase. At O, there will be maximum intensity.
There will be maximum intensity at P.
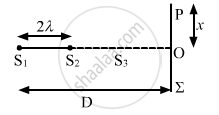
\[∆ S_1 PO\] and \[∆ S_2 PO\] are right-angled triangles.
So,
\[\left( S_1 P \right)^2 - \left( S_2 P \right)^2 \]
\[ = \left[ D^2 + x^2 \right] - \left[ \left( D - 2\lambda \right)^2 + x^2 \right]^2 \]
\[ = 4\lambda D + 4 \lambda^2 = 4\lambda D\]
\[( \lambda^2 \text { is small and can be neglected })\]
\[ \Rightarrow \left( S_1 P + S_2 P \right)\left( S_1 P - S_2 P \right) = 4\lambda D\]
\[ \Rightarrow \left( S_1 P - S_2 P \right) = \frac{4\lambda D}{\left( S_1 P + S_2 P \right)}\]
\[ \Rightarrow S_1 P - S_2 P = \frac{4\lambda D}{2\sqrt{x^2 + D^2}}\]
For constructive interference, path difference = n \[\lambda\]
So,
\[\Rightarrow S_1 P - S_2 P = \frac{4\lambda D}{2\sqrt{x^2 + D^2}} = n\lambda\]
\[ \Rightarrow \frac{2D}{\sqrt{x^2 + D^2}} = n\]
\[ \Rightarrow n^2 ( x^2 + D^2 ) = 4 D^2 \]
\[ \Rightarrow n^2 x^2 + n^2 D^2 = 4 D^2 \]
\[ \Rightarrow n^2 x^2 = 4 D^2 - n^2 D^2 \]
\[ \Rightarrow n^2 x^2 = D^2 \left( 4 - n^2 \right)\]
\[ \Rightarrow x = \frac{D}{n}\sqrt{4 - n^2}\]
\[\text { When n = 1 }, \]
\[x = \sqrt{3}D (\text { 1st order }) . \]
\[\text { When n } = 2, \]
\[x = 0 \ (\text { 2nd order }) . \]
So, when x = \[\sqrt{3}D\] , the intensity at P is equal to the intensity at O.
APPEARS IN
संबंधित प्रश्न
The wavelengths of two sound waves in air are `81/173`m and `81/170`m. They produce 10 beats per second. Calculate the velocity of sound in air
Can you hear your own words if you are standing in a perfect vacuum? Can you hear your friend in the same conditions?
Two tuning forks vibrate with the same amplitude but the frequency of the first is double the frequency of the second. Which fork produces more intense sound in air?
When you speak to your friend, which of the following parameters have a unique value in the sound produced?
An electrically maintained tuning fork vibrates with constant frequency and constant amplitude. If the temperature of the surrounding air increases but pressure remains constant, the produced will have
(a) larger wavelength
(b) larger frequency
(c) larger velocity
(d) larger time period.
A source of sound moves towards an observer.
A sources of sound operates at 2.0 kHz, 20 W emitting sound uniformly in all directions. The speed of sound in air is 340 m s−1 and the density of air is 1.2 kg m −3. (a) What is the intensity at a distance of 6.0 m from the source? (b) What will be the pressure amplitude at this point? (c) What will be the displacement amplitude at this point?
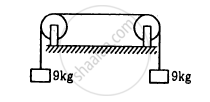
The length of the wire shown in figure between the pulley is 1⋅5 m and its mass is 12⋅0 g. Find the frequency of vibration with which the wire vibrates in two loops leaving the middle point of the wire between the pulleys at rest.
A particular guitar wire is 30⋅0 cm long and vibrates at a frequency of 196 Hz when no finger is placed on it. The next higher notes on the scale are 220 Hz, 247 Hz, 262 Hz and 294 Hz. How far from the end of the string must the finger be placed to play these notes?
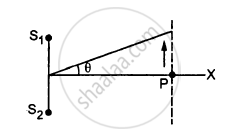
Two speakers S1 and S2, driven by the same amplifier, are placed at y = 1.0 m and y = −1.0 m(See figure). The speakers vibrate in phase at 600 Hz. A man stands at a point on the X-axis at a very large distance from the origin and starts moving parallel to the Y-axis. The speed of sound in air is 330 m s−1. (a) At what angle θ will the intensity of sound drop to a minimum for the first time? (b) At what angle will he hear a maximum of sound intensity for the first time? (c) If he continues to walk along the line, how many more can he hear?
A cylindrical tube, open at both ends, has a fundamental frequency v. The tube is dipped vertically in water so that half of its length is inside the water. The new fundamental frequency is
A tuning fork of frequency 256 Hz produces 4 beats per second with a wire of length 25 cm vibrating in its fundamental mode. The beat frequency decreases when the length is slightly shortened. What could be the minimum length by which the wire we shortened so that it produces no beats with the tuning fork?
A sound source, fixed at the origin, is continuously emitting sound at a frequency of 660 Hz. The sound travels in air at a speed of 330 m s−1. A listener is moving along the lien x= 336 m at a constant speed of 26 m s−1. Find the frequency of the sound as observed by the listener when he is (a) at y = − 140 m, (b) at y = 0 and (c) at y = 140 m.
A car moves with a speed of 54 km h−1 towards a cliff. The horn of the car emits sound of frequency 400 Hz at a speed of 335 m s−1. (a) Find the wavelength of the sound emitted by the horn in front of the car. (b) Find the wavelength of the wave reflected from the cliff. (c) What frequency does a person sitting in the car hear for the reflected sound wave? (d) How many beats does he hear in 10 seconds between the sound coming directly from the horn and that coming after the reflection?
A source of sound emitting a 1200 Hz note travels along a straight line at a speed of 170 m s−1. A detector is placed at a distance 200 m from the line of motion of the source. (a) Find the frequency of sound receive by the detector at the instant when the source gets closest to it. (b) Find the distance between the source and the detector at the instant in detects the frequency 1200 Hz. Velocity of sound in air = 340 m s−1.
For the propagation of longitudinal waves, the medium must have
- elasticity
- mass
- inertia
- force of cohesion
With propagation of longitudinal waves through a medium, the quantity transmitted is ______.
In the wave equation
`y = 0.5sin (2pi)/lambda(400t - x)m`
the velocity of the wave will be ______.
A transverse wave is represented by y = 2sin (ωt - kx) cm. The value of wavelength (in cm) for which the wave velocity becomes equal to the maximum particle velocity, will be ______.
