Advertisements
Advertisements
प्रश्न
A particular guitar wire is 30⋅0 cm long and vibrates at a frequency of 196 Hz when no finger is placed on it. The next higher notes on the scale are 220 Hz, 247 Hz, 262 Hz and 294 Hz. How far from the end of the string must the finger be placed to play these notes?
उत्तर
Given:
Length of the guitar wire (L1) = 30.0 cm = 0.30 m
Frequency, when no finger is placed on it, (f1) =196 Hz
And (f2) =220 Hz, (f3) = 247 Hz, (f4) = 262 Hz and (f5) = 294 Hz
The velocity is constant for a medium.
We have:
\[f \propto \left( \frac{1}{L} \right)\]
\[\Rightarrow \frac{f_1}{f_2} = \frac{L_2}{L_1}\]
\[ \Rightarrow \frac{196}{220} = \frac{L_2}{0 . 3}\]
\[ \Rightarrow L_2 = \frac{196 \times 0 . 3}{220} = 0 . 267 m\]
\[ \Rightarrow L_2 = 26 . 7 cm\]
Again,
\[f_3 = 247 Hz\]
\[\Rightarrow \frac{f_3}{f_1} = \frac{L_1}{L_3}\]
\[ \Rightarrow \frac{247}{196} = \frac{0 . 3}{L_3}\]
\[ \Rightarrow L_3 = 196 \times \frac{0 . 3}{247} = 0 . 238 m\]
\[ \Rightarrow L_3 = 23 . 8 cm\]
\[Similarly, L_4 = 196 \times \frac{0 . 3}{262} = 0 . 224 m\]
\[ \Rightarrow L_4 = 22 . 4 cm\]
\[And, L_5 = 20 \text{ cm }\]
APPEARS IN
संबंधित प्रश्न
A wave is represented by an equation \[y = c_1 \sin \left( c_2 x + c_3 t \right)\] In which direction is the wave going? Assume that \[c_1 , c_2\] \[c_3\] are all positive.
Two loudspeakers are arranged facing each other at some distance. Will a person standing behind one of the loudspeakers clearly hear the sound of the other loudspeaker or the clarity will be seriously damaged because of the 'collision' of the two sounds in between?
The bulk modulus and the density of water are greater than those of air. With this much of information, we can say that velocity of sound in air
A tuning fork sends sound waves in air. If the temperature of the air increases, which of the following parameters will change?
A tuning fork of frequency 512 Hz is vibrated with a sonometer wire and 6 beats per second are heard. The beat frequency reduces if the tension in the string is slightly increased. The original frequency of vibration of the string is
A source of sound moves towards an observer.
A person can hear sound waves in the frequency range 20 Hz to 20 kHz. Find the minimum and the maximum wavelengths of sound that is audible to the person. The speed of sound is 360 m s−1.
The equation of a travelling sound wave is y = 6.0 sin (600 t − 1.8 x) where y is measured in 10−5 m, t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed.
If the sound level in a room is increased from 50 dB to 60 dB, by what factor is the pressure amplitude increased?
The noise level in a classroom in absence of the teacher is 50 dB when 50 students are present. Assuming that on the average each student output same sound energy per second, what will be the noise level if the number of students is increased to 100?
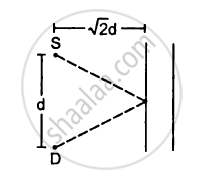
A source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance \[\sqrt{2}d\] from the source and the detector as shown in figure. The source emits a wave of wavelength = d/2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave?
The two sources of sound, S1 and S2, emitting waves of equal wavelength 20.0 cm, are placed with a separation of 20.0 cm between them. A detector can be moved on a line parallel to S1 S2 and at a distance of 20.0 cm from it. Initially, the detector is equidistant from the two sources. Assuming that the waves emitted by the sources are in detector should be shifted to detect a minimum of sound.
Three sources of sound S1, S2 and S3 of equal intensity are placed in a straight line with S1S2 = S2S3. At a point P, far away from the sources, the wave coming from S2 is 120° ahead in phase of that from S1. Also, the wave coming from S3 is 120° ahead of that from S2. What would be the resultant intensity of sound at P?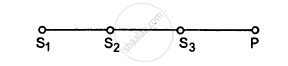
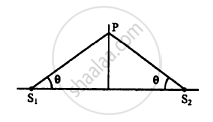
Two sources of sound S1 and S2 vibrate at same frequency and are in phase. The intensity of sound detected at a point P as shown in the figure is I0. (a) If θ equals 45°, what will be the intensity of sound detected at this point if one of the sources is switched off? (b) What will be the answer of the previous part if θ = 60°?
A small source of sound oscillates in simple harmonic motion with an amplitude of 17 cm. A detector is placed along the line of motion of the source. The source emits a sound of frequency 800 Hz which travels at a speed of 340 m s−1. If the width of the frequency band detected by the detector is 8 Hz, find the time period of the source.
A source of sound emitting a 1200 Hz note travels along a straight line at a speed of 170 m s−1. A detector is placed at a distance 200 m from the line of motion of the source. (a) Find the frequency of sound receive by the detector at the instant when the source gets closest to it. (b) Find the distance between the source and the detector at the instant in detects the frequency 1200 Hz. Velocity of sound in air = 340 m s−1.
Which of the following statements are true for wave motion?
In an experiment to determine the velocity of sound in air at room temperature using a resonance tube, the first resonance is observed when the air column has a length of 20.0 cm for a tuning fork of frequency 400 Hz is used. The velocity of the sound at room temperature is 336 ms-1. The third resonance is observed when the air column has a length of ______ cm.
In the wave equation
`y = 0.5sin (2pi)/lambda(400t - x)m`
the velocity of the wave will be ______.
