Advertisements
Advertisements
प्रश्न
A particular guitar wire is 30⋅0 cm long and vibrates at a frequency of 196 Hz when no finger is placed on it. The next higher notes on the scale are 220 Hz, 247 Hz, 262 Hz and 294 Hz. How far from the end of the string must the finger be placed to play these notes?
उत्तर
Given:
Length of the guitar wire (L1) = 30.0 cm = 0.30 m
Frequency, when no finger is placed on it, (f1) =196 Hz
And (f2) =220 Hz, (f3) = 247 Hz, (f4) = 262 Hz and (f5) = 294 Hz
The velocity is constant for a medium.
We have:
\[f \propto \left( \frac{1}{L} \right)\]
\[\Rightarrow \frac{f_1}{f_2} = \frac{L_2}{L_1}\]
\[ \Rightarrow \frac{196}{220} = \frac{L_2}{0 . 3}\]
\[ \Rightarrow L_2 = \frac{196 \times 0 . 3}{220} = 0 . 267 m\]
\[ \Rightarrow L_2 = 26 . 7 cm\]
Again,
\[f_3 = 247 Hz\]
\[\Rightarrow \frac{f_3}{f_1} = \frac{L_1}{L_3}\]
\[ \Rightarrow \frac{247}{196} = \frac{0 . 3}{L_3}\]
\[ \Rightarrow L_3 = 196 \times \frac{0 . 3}{247} = 0 . 238 m\]
\[ \Rightarrow L_3 = 23 . 8 cm\]
\[Similarly, L_4 = 196 \times \frac{0 . 3}{262} = 0 . 224 m\]
\[ \Rightarrow L_4 = 22 . 4 cm\]
\[And, L_5 = 20 \text{ cm }\]
APPEARS IN
संबंधित प्रश्न
Explain what is Doppler effect in sound
The wavelengths of two sound waves in air are `81/173`m and `81/170`m. They produce 10 beats per second. Calculate the velocity of sound in air
What is the smallest positive phase constant which is equivalent to 7⋅5 π?
When we clap our hands, the sound produced is best described by Here p denotes the change in pressure from the equilibrium value.
The bulk modulus and the density of water are greater than those of air. With this much of information, we can say that velocity of sound in air
Two sound waves move in the same direction in the same medium. The pressure amplitudes of the waves are equal but the wavelength of the first wave is double the second. Let the average power transmitted across a cross section by the first wave be P1 and that by the second wave be P2. Then
When two waves with same frequency and constant phase difference interfere,
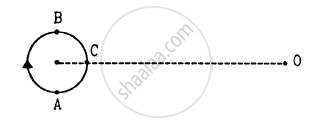
A small source of sounds moves on a circle as shown in figure and an observer is sitting at O. Let \[v_1, v_2, v_3\] be the frequencies heard when the source is at A, B and C respectively.
An electrically maintained tuning fork vibrates with constant frequency and constant amplitude. If the temperature of the surrounding air increases but pressure remains constant, the produced will have
(a) larger wavelength
(b) larger frequency
(c) larger velocity
(d) larger time period.
A listener is at rest with respect to the source of sound. A wind starts blowing along the line joining the source and the observer. Which of the following quantities do not change?
(a) Frequency
(b) Velocity of sound
(c) Wavelength
(d) Time period
A sound wave frequency 100 Hz is travelling in air. The speed of sound in air is 350 m s−1. (a) By how much is the phase changed at a given point in 2.5 ms? (b) What is the phase difference at a given instant between two points separated by a distance of 10.0 cm along the direction of propagation?
Two point sources of sound are kept at a separation of 10 cm. They vibrate in phase to produce waves of wavelength 5.0 cm. What would be the phase difference between the two waves arriving at a point 20 cm from one source (a) on the line joining the sources and (b) on the perpendicular bisector of the line joining the sources?
At what temperature will the speed of sound be double of its value at 0°C?
If the intensity of sound is doubled, by how many decibels does the sound level increase?
A string, fixed at both ends, vibrates in a resonant mode with a separation of 2⋅0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1⋅6 cm. Find the length of the string.
Three sources of sound S1, S2 and S3 of equal intensity are placed in a straight line with S1S2 = S2S3. At a point P, far away from the sources, the wave coming from S2 is 120° ahead in phase of that from S1. Also, the wave coming from S3 is 120° ahead of that from S2. What would be the resultant intensity of sound at P?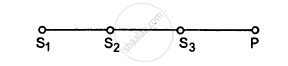
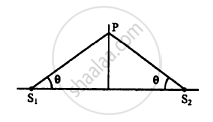
Two sources of sound S1 and S2 vibrate at same frequency and are in phase. The intensity of sound detected at a point P as shown in the figure is I0. (a) If θ equals 45°, what will be the intensity of sound detected at this point if one of the sources is switched off? (b) What will be the answer of the previous part if θ = 60°?
A traffic policeman standing on a road sounds a whistle emitting the main frequency of 2.00 kHz. What could be the apparent frequency heard by a scooter-driver approaching the policeman at a speed of 36.0 km h−1? Speed of sound in air = 340 m s−1.
Two electric trains run at the same speed of 72 km h−1 along the same track and in the same direction with separation of 2.4 km between them. The two trains simultaneously sound brief whistles. A person is situated at a perpendicular distance of 500 m from the track and is equidistant from the two trains at the instant of the whistling. If both the whistles were at 500 Hz and the speed of sound in air is 340 m s−1, find the frequencies heard by the person.
In the wave equation
`y = 0.5sin (2pi)/lambda(400t - x)m`
the velocity of the wave will be ______.
