Advertisements
Advertisements
प्रश्न
A traffic policeman standing on a road sounds a whistle emitting the main frequency of 2.00 kHz. What could be the apparent frequency heard by a scooter-driver approaching the policeman at a speed of 36.0 km h−1? Speed of sound in air = 340 m s−1.
उत्तर
Velocity of sound in air v = 340 ms−1
Velocity of scooter-driver \[v_o\]= 36 kmh−1 =
\[36 \times \frac{5}{18} = 10 {\text { ms }}^{- 1}\]
Frequency of sound of whistle \[f_o\]= 2 kHz
Apparent frequency \[\left( f \right)\] heard by the scooter-driver approaching the policeman is given by :
\[f = \left( \frac{v + v_o}{v} \right) \times f_o\]
\[f = \left( \frac{340 + 10}{340} \right) \times 2\]
\[ = \frac{350 \times 2}{340} \text { kHz }\]
\[ = 2 . 06 \text{ kHz }\]
APPEARS IN
संबंधित प्रश्न
A wave is represented by an equation \[y = c_1 \sin \left( c_2 x + c_3 t \right)\] In which direction is the wave going? Assume that \[c_1 , c_2\] \[c_3\] are all positive.
The equation \[y = A \sin^2 \left( kx - \omega t \right)\]
represents a wave motion with
When we clap our hands, the sound produced is best described by Here p denotes the change in pressure from the equilibrium value.
A person can hear sound waves in the frequency range 20 Hz to 20 kHz. Find the minimum and the maximum wavelengths of sound that is audible to the person. The speed of sound is 360 m s−1.
Two point sources of sound are kept at a separation of 10 cm. They vibrate in phase to produce waves of wavelength 5.0 cm. What would be the phase difference between the two waves arriving at a point 20 cm from one source (a) on the line joining the sources and (b) on the perpendicular bisector of the line joining the sources?
The sound level at a point 5.0 m away from a point source is 40 dB. What will be the level at a point 50 m away from the source?
A string, fixed at both ends, vibrates in a resonant mode with a separation of 2⋅0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1⋅6 cm. Find the length of the string.
If the sound level in a room is increased from 50 dB to 60 dB, by what factor is the pressure amplitude increased?
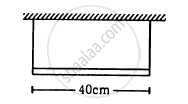
A uniform horizontal rod of length 40 cm and mass 1⋅2 kg is supported by two identical wires as shown in figure. Where should a mass of 4⋅8 kg be placed on the rod so that the same tuning fork may excite the wire on left into its fundamental vibrations and that on right into its first overtone? Take g = 10 m s−2.
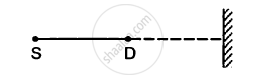
A source of sound S and detector D are placed at some distance from one another. a big cardboard is placed near hte detector and perpendicular to the line SD as shown in figure. It is gradually moved away and it is found that the intensity changes from a maximum to a minimum as the board is moved through a distance of 20 cm. Find the frequency of the sound emitted. Velocity of sound in air is 336 m s−1.
The separation between a node and the next antinode in a vibrating air column is 25 cm. If the speed of sound in air is 340 m s−1, find the frequency of vibration of the air column.
The first overtone frequency of a closed organ pipe P1 is equal to the fundamental frequency of a open organ pipe P2. If the length of the pipe P1 is 30 cm, what will be the length of P2?
A tuning fork produces 4 beats per second with another tuning fork of frequency 256 Hz. The first one is now loaded with a little wax and the beat frequency is found to increase to 6 per second. What was the original frequency of the tuning fork?
A piano wire A vibrates at a fundamental frequency of 600 Hz. A second identical wire Bproduces 6 beats per second with it when the tension in A is slightly increased. Find the the ratio of the tension in A to the tension in B.
A tuning fork of frequency 256 Hz produces 4 beats per second with a wire of length 25 cm vibrating in its fundamental mode. The beat frequency decreases when the length is slightly shortened. What could be the minimum length by which the wire we shortened so that it produces no beats with the tuning fork?
A car moves with a speed of 54 km h−1 towards a cliff. The horn of the car emits sound of frequency 400 Hz at a speed of 335 m s−1. (a) Find the wavelength of the sound emitted by the horn in front of the car. (b) Find the wavelength of the wave reflected from the cliff. (c) What frequency does a person sitting in the car hear for the reflected sound wave? (d) How many beats does he hear in 10 seconds between the sound coming directly from the horn and that coming after the reflection?
With propagation of longitudinal waves through a medium, the quantity transmitted is ______.
In the wave equation
`y = 0.5sin (2pi)/lambda(400t - x)m`
the velocity of the wave will be ______.
