Advertisements
Advertisements
प्रश्न
A tuning fork of frequency 256 Hz produces 4 beats per second with a wire of length 25 cm vibrating in its fundamental mode. The beat frequency decreases when the length is slightly shortened. What could be the minimum length by which the wire we shortened so that it produces no beats with the tuning fork?
उत्तर
Given:
Length of the wire l = 25 cm = 25 × 10−2 m
Frequency of tuning fork \[f\] = 256 Hz
Let T be the tension and m the mass per unit length of the wire.
Frequency of the fundamental note in the wire is given by : \[f = \frac{1}{2l}\sqrt{\frac{T}{m}}\]
It is clear from the above relation that by shortening the length of the wire, the frequency of the vibrations increases.
In the first case :
\[256 = \frac{1}{2 \times 25 \times {10}^{- 2}}\sqrt{\left( \frac{T}{m} \right)} . . . (1)\]
Let the length of the wire be l1, after it is slightly shortened.
As the vibrating wire produces 4 beats with 256 Hz, its frequency must be 252 Hz or 260 Hz. Again, its frequency must be 252 Hz, as the beat frequency decreases on shortening the wire.
In the second case :
\[\Rightarrow 252 = \frac{1}{2 \times I_1}\sqrt{\frac{T}{m}} . . . (2)\]
Dividing (2) by (1), we have:
\[\frac{252}{256} = \frac{I_1}{25 \times {10}^{- 2}}\]
\[ \Rightarrow I_1 = \frac{252 \times 25 \times {10}^{- 2}}{256}\]
\[ = 0 . 24609 \text{ m }\]
So, it must be shortened by (25 − 24.61)
= 0.39 cm.
APPEARS IN
संबंधित प्रश्न
Explain what is Doppler effect in sound
A wave is represented by an equation \[y = c_1 \sin \left( c_2 x + c_3 t \right)\] In which direction is the wave going? Assume that \[c_1 , c_2\] \[c_3\] are all positive.
What is the smallest positive phase constant which is equivalent to 7⋅5 π?
Two tuning forks vibrate with the same amplitude but the frequency of the first is double the frequency of the second. Which fork produces more intense sound in air?
A small source of sounds moves on a circle as shown in figure and an observer is sitting at O. Let \[v_1, v_2, v_3\] be the frequencies heard when the source is at A, B and C respectively.
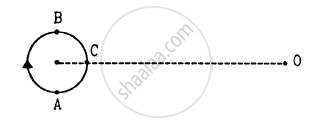
A source of sound moves towards an observer.
Find the minimum and maximum wavelengths of sound in water that is in the audible range (20−20000 Hz) for an average human ear. Speed of sound in water = 1450 m s−1.
A sound wave frequency 100 Hz is travelling in air. The speed of sound in air is 350 m s−1. (a) By how much is the phase changed at a given point in 2.5 ms? (b) What is the phase difference at a given instant between two points separated by a distance of 10.0 cm along the direction of propagation?
A sources of sound operates at 2.0 kHz, 20 W emitting sound uniformly in all directions. The speed of sound in air is 340 m s−1 and the density of air is 1.2 kg m −3. (a) What is the intensity at a distance of 6.0 m from the source? (b) What will be the pressure amplitude at this point? (c) What will be the displacement amplitude at this point?
The intensity of sound from a point source is 1.0 × 10−8 W m−2 at a distance of 5.0 m from the source. What will be the intensity at a distance of 25 m from the source?
If the sound level in a room is increased from 50 dB to 60 dB, by what factor is the pressure amplitude increased?
A string of length L fixed at both ends vibrates in its fundamental mode at a frequency ν and a maximum amplitude A. (a)
- Find the wavelength and the wave number k.
- Take the origin at one end of the string and the X-axis along the string. Take the Y-axis along the direction of the displacement. Take t = 0 at the instant when the middle point of the string passes through its mean position and is going towards the positive y-direction. Write the equation describing the standing wave.
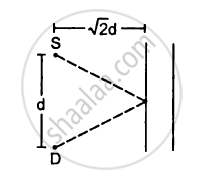
A source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance \[\sqrt{2}d\] from the source and the detector as shown in figure. The source emits a wave of wavelength = d/2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave?
Two speakers S1 and S2, driven by the same amplifier, are placed at y = 1.0 m and y = −1.0 m(See figure). The speakers vibrate in phase at 600 Hz. A man stands at a point on the X-axis at a very large distance from the origin and starts moving parallel to the Y-axis. The speed of sound in air is 330 m s−1. (a) At what angle θ will the intensity of sound drop to a minimum for the first time? (b) At what angle will he hear a maximum of sound intensity for the first time? (c) If he continues to walk along the line, how many more can he hear?
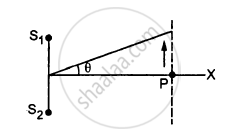
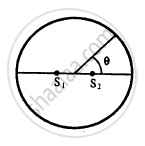
Figure shown two coherent sources S1 and S2 which emit sound of wavelength λ in phase. The separation between the sources is 3λ. A circular wire of large radius is placed in such way that S1,S2 is at the centre of the wire. Find the angular positions θ on the wire for which constructive interference takes place.
The separation between a node and the next antinode in a vibrating air column is 25 cm. If the speed of sound in air is 340 m s−1, find the frequency of vibration of the air column.
The first overtone frequency of a closed organ pipe P1 is equal to the fundamental frequency of a open organ pipe P2. If the length of the pipe P1 is 30 cm, what will be the length of P2?
A cylindrical tube, open at both ends, has a fundamental frequency v. The tube is dipped vertically in water so that half of its length is inside the water. The new fundamental frequency is
Two electric trains run at the same speed of 72 km h−1 along the same track and in the same direction with separation of 2.4 km between them. The two trains simultaneously sound brief whistles. A person is situated at a perpendicular distance of 500 m from the track and is equidistant from the two trains at the instant of the whistling. If both the whistles were at 500 Hz and the speed of sound in air is 340 m s−1, find the frequencies heard by the person.
A small speaker delivers 2W of audio output. At what distance from the speaker will one detect 120 dB intensity sound?
[Given reference intensity of sound as 10-12W/m2]
