Advertisements
Advertisements
Question
A tuning fork of frequency 256 Hz produces 4 beats per second with a wire of length 25 cm vibrating in its fundamental mode. The beat frequency decreases when the length is slightly shortened. What could be the minimum length by which the wire we shortened so that it produces no beats with the tuning fork?
Solution
Given:
Length of the wire l = 25 cm = 25 × 10−2 m
Frequency of tuning fork \[f\] = 256 Hz
Let T be the tension and m the mass per unit length of the wire.
Frequency of the fundamental note in the wire is given by : \[f = \frac{1}{2l}\sqrt{\frac{T}{m}}\]
It is clear from the above relation that by shortening the length of the wire, the frequency of the vibrations increases.
In the first case :
\[256 = \frac{1}{2 \times 25 \times {10}^{- 2}}\sqrt{\left( \frac{T}{m} \right)} . . . (1)\]
Let the length of the wire be l1, after it is slightly shortened.
As the vibrating wire produces 4 beats with 256 Hz, its frequency must be 252 Hz or 260 Hz. Again, its frequency must be 252 Hz, as the beat frequency decreases on shortening the wire.
In the second case :
\[\Rightarrow 252 = \frac{1}{2 \times I_1}\sqrt{\frac{T}{m}} . . . (2)\]
Dividing (2) by (1), we have:
\[\frac{252}{256} = \frac{I_1}{25 \times {10}^{- 2}}\]
\[ \Rightarrow I_1 = \frac{252 \times 25 \times {10}^{- 2}}{256}\]
\[ = 0 . 24609 \text{ m }\]
So, it must be shortened by (25 − 24.61)
= 0.39 cm.
APPEARS IN
RELATED QUESTIONS
Explain what is Doppler effect in sound
A wave is represented by an equation \[y = c_1 \sin \left( c_2 x + c_3 t \right)\] In which direction is the wave going? Assume that \[c_1 , c_2\] \[c_3\] are all positive.
Two tuning forks vibrate with the same amplitude but the frequency of the first is double the frequency of the second. Which fork produces more intense sound in air?
The bulk modulus and the density of water are greater than those of air. With this much of information, we can say that velocity of sound in air
A tuning fork of frequency 512 Hz is vibrated with a sonometer wire and 6 beats per second are heard. The beat frequency reduces if the tension in the string is slightly increased. The original frequency of vibration of the string is
A small source of sounds moves on a circle as shown in figure and an observer is sitting at O. Let \[v_1, v_2, v_3\] be the frequencies heard when the source is at A, B and C respectively.
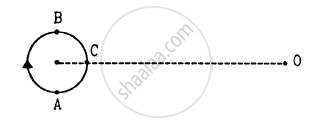
A listener is at rest with respect to the source of sound. A wind starts blowing along the line joining the source and the observer. Which of the following quantities do not change?
(a) Frequency
(b) Velocity of sound
(c) Wavelength
(d) Time period
A steel tube of length 1.00 m is struck at one end. A person with his ear closed to the other end hears the sound of the blow twice, one travelling through the body of the tube and the other through the air in the tube. Find the time gap between the two hearings. Use the table in the text for speeds of sound in various substances.
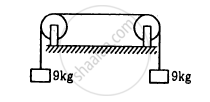
The length of the wire shown in figure between the pulley is 1⋅5 m and its mass is 12⋅0 g. Find the frequency of vibration with which the wire vibrates in two loops leaving the middle point of the wire between the pulleys at rest.
Sound with intensity larger than 120 dB appears pain full to a person. A small speaker delivers 2.0 W of audio output. How close can the person get to the speaker without hurting his ears?
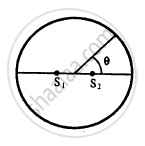
Figure shown two coherent sources S1 and S2 which emit sound of wavelength λ in phase. The separation between the sources is 3λ. A circular wire of large radius is placed in such way that S1,S2 is at the centre of the wire. Find the angular positions θ on the wire for which constructive interference takes place.
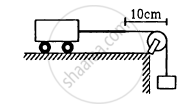
A heavy string is tied at one end to a movable support and to a light thread at the other end as shown in following figure. The thread goes over a fixed pulley and supports a weight to produce a tension. The lowest frequency with which the heavy string resonates is 120 Hz. If the movable support is pushed to the right by 10 cm so that the joint is placed on the pulley, what will be the minimum frequency at which the heavy string can resonate?
In a standing wave pattern in a vibrating air column, nodes are formed at a distance of 4.0 cm. If the speed of sound in air is 328 m s−1, what is the frequency of the source?
The fundamental frequency of a closed pipe is 293 Hz when the air in it is a temperature of 20°C. What will be its fundamental frequency when the temperature changes to 22°C?
Show that if the room temperature changes by a small amount from T to T + ∆T, the fundamental frequency of an organ pipe changes from v to v + ∆v, where \[\frac{∆ v}{v} = \frac{1}{2}\frac{∆ T}{T} .\]
A traffic policeman standing on a road sounds a whistle emitting the main frequency of 2.00 kHz. What could be the apparent frequency heard by a scooter-driver approaching the policeman at a speed of 36.0 km h−1? Speed of sound in air = 340 m s−1.
Two electric trains run at the same speed of 72 km h−1 along the same track and in the same direction with separation of 2.4 km between them. The two trains simultaneously sound brief whistles. A person is situated at a perpendicular distance of 500 m from the track and is equidistant from the two trains at the instant of the whistling. If both the whistles were at 500 Hz and the speed of sound in air is 340 m s−1, find the frequencies heard by the person.
A train running at 108 km h−1 towards east whistles at a dominant frequency of 500 Hz. Speed of sound in air is 340 m/s. What frequency will a passenger sitting near the open window hear? (b) What frequency will a person standing near the track hear whom the train has just passed? (c) A wind starts blowing towards east at a speed of 36 km h−1. Calculate the frequencies heard by the passenger in the train and by the person standing near the track.
A car moves with a speed of 54 km h−1 towards a cliff. The horn of the car emits sound of frequency 400 Hz at a speed of 335 m s−1. (a) Find the wavelength of the sound emitted by the horn in front of the car. (b) Find the wavelength of the wave reflected from the cliff. (c) What frequency does a person sitting in the car hear for the reflected sound wave? (d) How many beats does he hear in 10 seconds between the sound coming directly from the horn and that coming after the reflection?
The speed of a wave in a string is 20 m/s and the frequency is 50 Hz. The phase difference between two points on the string 10 cm apart will be ______.
