Advertisements
Advertisements
Question
A train running at 108 km h−1 towards east whistles at a dominant frequency of 500 Hz. Speed of sound in air is 340 m/s. What frequency will a passenger sitting near the open window hear? (b) What frequency will a person standing near the track hear whom the train has just passed? (c) A wind starts blowing towards east at a speed of 36 km h−1. Calculate the frequencies heard by the passenger in the train and by the person standing near the track.
Solution
Given:
Velocity of sound in air v = 340 m/s
Velocity of source vs = 108 `\text{ kmh}^\(-)`1 =\[\frac{108 \times 1000}{60 \times 60} = 30 {\text { ms }}^{- 1}\]
Frequency of the source \[n_0\]= 500 Hz
(a) Since the velocity of the passenger with respect to the train is zero, he will hear at a frequency of 500 Hz.
(b) Since the observer is moving away from the source while the source is at rest:
Velocity of observer \[v_o\]= 0
Frequency of sound heard by person standing near the track is given by:
\[n = \left( \frac{v}{v + v_s} \right) n_0 \]
Substituting the values, we get:
\[n = \frac{340}{340 + 30} \times 500 = 459 \text{ Hz }\]
(c) When medium (wind) starts blowing towards the east:
Velocity of medium vm = 36 `\text { kmh}^\(-)`1 =\[36 \times \frac{5}{18} = 10 {\text { ms }}^{- 1}\]
However, frequency heard by person standing near the track is given by:
\[n = \frac{\left( v + v_m \right)}{\left( v + v_m \right) + v_s} \times n_0 \]
\[ = \frac{\left( 340 + 10 \right)}{\left( 340 + 10 \right) + 30} \times 500\]
\[ = 458 \text{ Hz }\]
APPEARS IN
RELATED QUESTIONS
The equation \[y = A \sin^2 \left( kx - \omega t \right)\]
represents a wave motion with
Can you hear your own words if you are standing in a perfect vacuum? Can you hear your friend in the same conditions?
A sound wave frequency 100 Hz is travelling in air. The speed of sound in air is 350 m s−1. (a) By how much is the phase changed at a given point in 2.5 ms? (b) What is the phase difference at a given instant between two points separated by a distance of 10.0 cm along the direction of propagation?
Two point sources of sound are kept at a separation of 10 cm. They vibrate in phase to produce waves of wavelength 5.0 cm. What would be the phase difference between the two waves arriving at a point 20 cm from one source (a) on the line joining the sources and (b) on the perpendicular bisector of the line joining the sources?
At what temperature will the speed of sound be double of its value at 0°C?
Calculate the bulk modulus of air from the following data about a sound wave of wavelength 35 cm travelling in air. The pressure at a point varies between (1.0 × 105 ± 14) Pa and the particles of the air vibrate in simple harmonic motion of amplitude 5.5 × 10−6 m.
Sound with intensity larger than 120 dB appears pain full to a person. A small speaker delivers 2.0 W of audio output. How close can the person get to the speaker without hurting his ears?
A particular guitar wire is 30⋅0 cm long and vibrates at a frequency of 196 Hz when no finger is placed on it. The next higher notes on the scale are 220 Hz, 247 Hz, 262 Hz and 294 Hz. How far from the end of the string must the finger be placed to play these notes?
A uniform horizontal rod of length 40 cm and mass 1⋅2 kg is supported by two identical wires as shown in figure. Where should a mass of 4⋅8 kg be placed on the rod so that the same tuning fork may excite the wire on left into its fundamental vibrations and that on right into its first overtone? Take g = 10 m s−2.
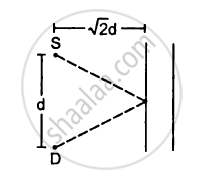
A source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance \[\sqrt{2}d\] from the source and the detector as shown in figure. The source emits a wave of wavelength = d/2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave?
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The sound is detected by moving a detector on the screen ∑ at a distance D(>>λ) from the slit S1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.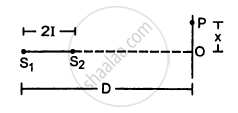
A tuning fork produces 4 beats per second with another tuning fork of frequency 256 Hz. The first one is now loaded with a little wax and the beat frequency is found to increase to 6 per second. What was the original frequency of the tuning fork?
Show that if the room temperature changes by a small amount from T to T + ∆T, the fundamental frequency of an organ pipe changes from v to v + ∆v, where \[\frac{∆ v}{v} = \frac{1}{2}\frac{∆ T}{T} .\]
A piano wire A vibrates at a fundamental frequency of 600 Hz. A second identical wire Bproduces 6 beats per second with it when the tension in A is slightly increased. Find the the ratio of the tension in A to the tension in B.
A traffic policeman standing on a road sounds a whistle emitting the main frequency of 2.00 kHz. What could be the apparent frequency heard by a scooter-driver approaching the policeman at a speed of 36.0 km h−1? Speed of sound in air = 340 m s−1.
A sound source, fixed at the origin, is continuously emitting sound at a frequency of 660 Hz. The sound travels in air at a speed of 330 m s−1. A listener is moving along the lien x= 336 m at a constant speed of 26 m s−1. Find the frequency of the sound as observed by the listener when he is (a) at y = − 140 m, (b) at y = 0 and (c) at y = 140 m.
A boy riding on a bicycle going at 12 km h−1 towards a vertical wall whistles at his dog on the ground. If the frequency of the whistle is 1600 Hz and the speed of sound in air is 330 m s−1, find (a) the frequency of the whistle as received by the wall (b) the frequency of the reflected whistle as received by the boy.
During propagation of a plane progressive mechanical wave ______.
- all the particles are vibrating in the same phase.
- amplitude of all the particles is equal.
- particles of the medium executes S.H.M.
- wave velocity depends upon the nature of the medium.
The speed of a wave in a string is 20 m/s and the frequency is 50 Hz. The phase difference between two points on the string 10 cm apart will be ______.
