Advertisements
Advertisements
Question
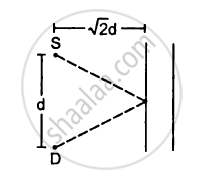
A source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance \[\sqrt{2}d\] from the source and the detector as shown in figure. The source emits a wave of wavelength = d/2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave?
Solution
Given:
Distance between the source and detector = d
Distance of cardboard from the source =\[\sqrt{2d}\]
Wavelength of the source \[\lambda\]= d/2
Path difference between sound waves received by the detector before shifting the cardboard:
\[2\left( \sqrt{\left( \frac{d}{2} \right)^2 + \left( \sqrt{2}d \right)^2} \right) - d\]
\[ \Rightarrow 2 \times \frac{3d}{2} - d\]
\[ \Rightarrow 2d\]
If the cardboard is shifted by a distance x, the path difference will be :
\[2\left( \sqrt{\left( \frac{d}{2} \right)^2 + \left( \sqrt{2d} + x \right)^2} \right) - d\]
According to the question,
\[2\sqrt{\left( \frac{d}{2} \right)^2 + \left( \sqrt{2}d + x \right)^2} - d = 2d + \frac{d}{4}\]
\[ \Rightarrow 2\sqrt{\left( \frac{d}{2} \right)^2 + \left( \sqrt{2}d + x \right)^2} - d = \frac{9d}{4}\]
\[ \Rightarrow 2\sqrt{\left( \frac{d}{2} \right)^2 + \left( \sqrt{2}d + x \right)^2} = \frac{9d}{4} + d = \frac{13d}{4}\]
\[ \Rightarrow \left( \frac{d}{2} \right)^2 + \left( \sqrt{2}d + x \right)^2 = \frac{169}{64} d^2 \]
\[ \Rightarrow \left( \sqrt{2}d + x \right)^2 = \frac{(169 - 16)}{64} d^2 = \frac{153}{64} d^2 \]
\[ \Rightarrow \sqrt{2}d + x = 1 . 54d\]
\[ \Rightarrow x = \left( 1 . 54 - 1 . 41 \right)d = 0 . 13d\]
APPEARS IN
RELATED QUESTIONS
The wavelengths of two sound waves in air are `81/173`m and `81/170`m. They produce 10 beats per second. Calculate the velocity of sound in air
Two tuning forks vibrate with the same amplitude but the frequency of the first is double the frequency of the second. Which fork produces more intense sound in air?
When we clap our hands, the sound produced is best described by Here p denotes the change in pressure from the equilibrium value.
An electrically maintained tuning fork vibrates with constant frequency and constant amplitude. If the temperature of the surrounding air increases but pressure remains constant, the produced will have
(a) larger wavelength
(b) larger frequency
(c) larger velocity
(d) larger time period.
The fundamental frequency of a vibrating organ pipe is 200 Hz.
(a) The first overtone is 400 Hz.
(b) The first overtone may be 400 Hz.
(c) The first overtone may be 600 Hz.
(d) 600 Hz is an overtone.
A person can hear sound waves in the frequency range 20 Hz to 20 kHz. Find the minimum and the maximum wavelengths of sound that is audible to the person. The speed of sound is 360 m s−1.
Sound waves from a loudspeaker spread nearly uniformly in all directions if the wavelength of the sound is much larger than the diameter of the loudspeaker. (a)Calculate the frequency for which the wavelength of sound in air is ten times the diameter of the speaker if the diameter is 20 cm. (b) Sound is essentially transmitted in the forward direction if the wavelength is much shorter than the diameter of the speaker. Calculate the frequency at which the wavelength of the sound is one tenth of the diameter of the speaker described above. Take the speed of sound to be 340 m/s.
The equation of a travelling sound wave is y = 6.0 sin (600 t − 1.8 x) where y is measured in 10−5 m, t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed.
At what temperature will the speed of sound be double of its value at 0°C?
The sound level at a point 5.0 m away from a point source is 40 dB. What will be the level at a point 50 m away from the source?
A string, fixed at both ends, vibrates in a resonant mode with a separation of 2⋅0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1⋅6 cm. Find the length of the string.
The noise level in a classroom in absence of the teacher is 50 dB when 50 students are present. Assuming that on the average each student output same sound energy per second, what will be the noise level if the number of students is increased to 100?
Three sources of sound S1, S2 and S3 of equal intensity are placed in a straight line with S1S2 = S2S3. At a point P, far away from the sources, the wave coming from S2 is 120° ahead in phase of that from S1. Also, the wave coming from S3 is 120° ahead of that from S2. What would be the resultant intensity of sound at P?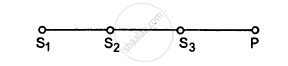
The first overtone frequency of a closed organ pipe P1 is equal to the fundamental frequency of a open organ pipe P2. If the length of the pipe P1 is 30 cm, what will be the length of P2?
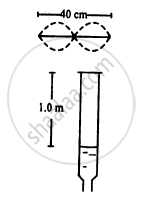
Consider the situation shown in the figure.The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 340 m s−1, find the tension in the wire.
A source of sound with adjustable frequency produces 2 beats per second with a tuning fork when its frequency is either 476 Hz of 480 Hz. What is the frequency of the tuning fork?
A piano wire A vibrates at a fundamental frequency of 600 Hz. A second identical wire Bproduces 6 beats per second with it when the tension in A is slightly increased. Find the the ratio of the tension in A to the tension in B.
During propagation of a plane progressive mechanical wave ______.
- all the particles are vibrating in the same phase.
- amplitude of all the particles is equal.
- particles of the medium executes S.H.M.
- wave velocity depends upon the nature of the medium.
In the wave equation
`y = 0.5sin (2pi)/lambda(400t - x)m`
the velocity of the wave will be ______.
