Advertisements
Advertisements
Question
The first overtone frequency of a closed organ pipe P1 is equal to the fundamental frequency of a open organ pipe P2. If the length of the pipe P1 is 30 cm, what will be the length of P2?
Solution
Given:
Length of closed organ pipe L1 = 30 cm
Length of open organ pipe L2 = ?
Let \[f_1\] and \[f_2\] be the frequencies of the closed and open organ pipes, respectively.
The first overtone frequency of a closed organ pipe P1 is given by
\[f_1 = \frac{3v}{4 L_1}\]
where v is the speed of sound in air.
On substituting the respective values, we get :
\[f_1 = \frac{3v}{4 \times 30}\]
Fundamental frequency of an open organ pipe is given by:
\[f_2 = \left( \frac{v}{2 L_2} \right)\]
As per the question,
\[f_1 = f_2 \]
\[ \left( \frac{3 \times v}{4 \times 30} \right) = \left( \frac{v}{2 L_2} \right)\]
\[ \Rightarrow L_2 = 20 \text { cm }\]
∴ The length of the pipe P2 will be 20 cm.
APPEARS IN
RELATED QUESTIONS
What is the smallest positive phase constant which is equivalent to 7⋅5 π?
If you are walking on the moon, can you hear the sound of stones cracking behind you? Can you hear the sound of your own footsteps?
The bulk modulus and the density of water are greater than those of air. With this much of information, we can say that velocity of sound in air
When you speak to your friend, which of the following parameters have a unique value in the sound produced?
The fundamental frequency of a vibrating organ pipe is 200 Hz.
(a) The first overtone is 400 Hz.
(b) The first overtone may be 400 Hz.
(c) The first overtone may be 600 Hz.
(d) 600 Hz is an overtone.
At what temperature will the speed of sound be double of its value at 0°C?
Calculate the bulk modulus of air from the following data about a sound wave of wavelength 35 cm travelling in air. The pressure at a point varies between (1.0 × 105 ± 14) Pa and the particles of the air vibrate in simple harmonic motion of amplitude 5.5 × 10−6 m.
If the intensity of sound is doubled, by how many decibels does the sound level increase?
The noise level in a classroom in absence of the teacher is 50 dB when 50 students are present. Assuming that on the average each student output same sound energy per second, what will be the noise level if the number of students is increased to 100?
A uniform horizontal rod of length 40 cm and mass 1⋅2 kg is supported by two identical wires as shown in figure. Where should a mass of 4⋅8 kg be placed on the rod so that the same tuning fork may excite the wire on left into its fundamental vibrations and that on right into its first overtone? Take g = 10 m s−2.
A string of length L fixed at both ends vibrates in its fundamental mode at a frequency ν and a maximum amplitude A. (a)
- Find the wavelength and the wave number k.
- Take the origin at one end of the string and the X-axis along the string. Take the Y-axis along the direction of the displacement. Take t = 0 at the instant when the middle point of the string passes through its mean position and is going towards the positive y-direction. Write the equation describing the standing wave.
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The sound is detected by moving a detector on the screen ∑ at a distance D(>>λ) from the slit S1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.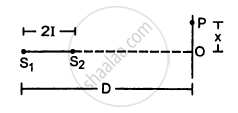
A source of sound with adjustable frequency produces 2 beats per second with a tuning fork when its frequency is either 476 Hz of 480 Hz. What is the frequency of the tuning fork?
Show that if the room temperature changes by a small amount from T to T + ∆T, the fundamental frequency of an organ pipe changes from v to v + ∆v, where \[\frac{∆ v}{v} = \frac{1}{2}\frac{∆ T}{T} .\]
A cylindrical tube, open at both ends, has a fundamental frequency v. The tube is dipped vertically in water so that half of its length is inside the water. The new fundamental frequency is
A small source of sound oscillates in simple harmonic motion with an amplitude of 17 cm. A detector is placed along the line of motion of the source. The source emits a sound of frequency 800 Hz which travels at a speed of 340 m s−1. If the width of the frequency band detected by the detector is 8 Hz, find the time period of the source.
A boy riding on his bike is going towards east at a speed of 4√2 m s−1. At a certain point he produces a sound pulse of frequency 1650 Hz that travels in air at a speed of 334 m s−1. A second boy stands on the ground 45° south of east from his. Find the frequency of the pulse as received by the second boy.
A car moves with a speed of 54 km h−1 towards a cliff. The horn of the car emits sound of frequency 400 Hz at a speed of 335 m s−1. (a) Find the wavelength of the sound emitted by the horn in front of the car. (b) Find the wavelength of the wave reflected from the cliff. (c) What frequency does a person sitting in the car hear for the reflected sound wave? (d) How many beats does he hear in 10 seconds between the sound coming directly from the horn and that coming after the reflection?
