Advertisements
Advertisements
Question
What is the smallest positive phase constant which is equivalent to 7⋅5 π?
Solution
Equation of the wave: y = A sin(kx − ωt + Φ)
Here, A is the amplitude, k is the wave number, ω is the angular frequency and Φ is the initial phase.
The argument of the sine is a phase, so the smallest positive phase constant should be
\[\sin\left( 7 . 5\pi \right) = \sin\left( 3 \times 2\pi + 1 . 5\pi \right)\]
\[ = \sin\left( 1 . 5\pi \right)\]
Therefore, the smallest positive phase constant is 1.5π.
APPEARS IN
RELATED QUESTIONS
The wavelengths of two sound waves in air are `81/173`m and `81/170`m. They produce 10 beats per second. Calculate the velocity of sound in air
Can you hear your own words if you are standing in a perfect vacuum? Can you hear your friend in the same conditions?
Two loudspeakers are arranged facing each other at some distance. Will a person standing behind one of the loudspeakers clearly hear the sound of the other loudspeaker or the clarity will be seriously damaged because of the 'collision' of the two sounds in between?
A tuning fork sends sound waves in air. If the temperature of the air increases, which of the following parameters will change?
When two waves with same frequency and constant phase difference interfere,
A person can hear sound waves in the frequency range 20 Hz to 20 kHz. Find the minimum and the maximum wavelengths of sound that is audible to the person. The speed of sound is 360 m s−1.
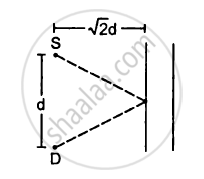
A source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance \[\sqrt{2}d\] from the source and the detector as shown in figure. The source emits a wave of wavelength = d/2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave?
Three sources of sound S1, S2 and S3 of equal intensity are placed in a straight line with S1S2 = S2S3. At a point P, far away from the sources, the wave coming from S2 is 120° ahead in phase of that from S1. Also, the wave coming from S3 is 120° ahead of that from S2. What would be the resultant intensity of sound at P?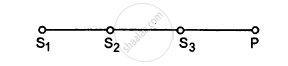
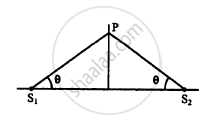
Two sources of sound S1 and S2 vibrate at same frequency and are in phase. The intensity of sound detected at a point P as shown in the figure is I0. (a) If θ equals 45°, what will be the intensity of sound detected at this point if one of the sources is switched off? (b) What will be the answer of the previous part if θ = 60°?
A source of sound with adjustable frequency produces 2 beats per second with a tuning fork when its frequency is either 476 Hz of 480 Hz. What is the frequency of the tuning fork?
A cylindrical tube, open at both ends, has a fundamental frequency v. The tube is dipped vertically in water so that half of its length is inside the water. The new fundamental frequency is
A piano wire A vibrates at a fundamental frequency of 600 Hz. A second identical wire Bproduces 6 beats per second with it when the tension in A is slightly increased. Find the the ratio of the tension in A to the tension in B.
A small source of sound oscillates in simple harmonic motion with an amplitude of 17 cm. A detector is placed along the line of motion of the source. The source emits a sound of frequency 800 Hz which travels at a speed of 340 m s−1. If the width of the frequency band detected by the detector is 8 Hz, find the time period of the source.
A car moves with a speed of 54 km h−1 towards a cliff. The horn of the car emits sound of frequency 400 Hz at a speed of 335 m s−1. (a) Find the wavelength of the sound emitted by the horn in front of the car. (b) Find the wavelength of the wave reflected from the cliff. (c) What frequency does a person sitting in the car hear for the reflected sound wave? (d) How many beats does he hear in 10 seconds between the sound coming directly from the horn and that coming after the reflection?
A small source of sound S of frequency 500 Hz is attached to the end of a light string and is whirled in a vertical circle of radius 1.6 m. The string just remains tight when the source is at the highest point. (a) An observer is located in the same vertical plane at a large distance and at the same height as the centre of the circle. The speed of sound in air = 330 m s−1 and g = 10 m s−2. Find the maximum frequency heard by the observer. (b) An observer is situated at a large distance vertically above the centre of the circle. Find the frequency heard by the observer corresponding to the sound emitted by the source when it is at the same height as the centre.
Equation of a plane progressive wave is given by `y = 0.6 sin 2π (t - x/2)`. On reflection from a denser medium its amplitude becomes 2/3 of the amplitude of the incident wave. The equation of the reflected wave is ______.
During propagation of a plane progressive mechanical wave ______.
- all the particles are vibrating in the same phase.
- amplitude of all the particles is equal.
- particles of the medium executes S.H.M.
- wave velocity depends upon the nature of the medium.
In the wave equation
`y = 0.5sin (2pi)/lambda(400t - x)m`
the velocity of the wave will be ______.
A transverse wave is represented by y = 2sin (ωt - kx) cm. The value of wavelength (in cm) for which the wave velocity becomes equal to the maximum particle velocity, will be ______.
A small speaker delivers 2W of audio output. At what distance from the speaker will one detect 120 dB intensity sound?
[Given reference intensity of sound as 10-12W/m2]
