Advertisements
Advertisements
प्रश्न
What is the smallest positive phase constant which is equivalent to 7⋅5 π?
उत्तर
Equation of the wave: y = A sin(kx − ωt + Φ)
Here, A is the amplitude, k is the wave number, ω is the angular frequency and Φ is the initial phase.
The argument of the sine is a phase, so the smallest positive phase constant should be
\[\sin\left( 7 . 5\pi \right) = \sin\left( 3 \times 2\pi + 1 . 5\pi \right)\]
\[ = \sin\left( 1 . 5\pi \right)\]
Therefore, the smallest positive phase constant is 1.5π.
APPEARS IN
संबंधित प्रश्न
The equation \[y = A \sin^2 \left( kx - \omega t \right)\]
represents a wave motion with
The bulk modulus and the density of water are greater than those of air. With this much of information, we can say that velocity of sound in air
An electrically maintained tuning fork vibrates with constant frequency and constant amplitude. If the temperature of the surrounding air increases but pressure remains constant, the produced will have
(a) larger wavelength
(b) larger frequency
(c) larger velocity
(d) larger time period.
The fundamental frequency of a vibrating organ pipe is 200 Hz.
(a) The first overtone is 400 Hz.
(b) The first overtone may be 400 Hz.
(c) The first overtone may be 600 Hz.
(d) 600 Hz is an overtone.
A steel tube of length 1.00 m is struck at one end. A person with his ear closed to the other end hears the sound of the blow twice, one travelling through the body of the tube and the other through the air in the tube. Find the time gap between the two hearings. Use the table in the text for speeds of sound in various substances.
Two point sources of sound are kept at a separation of 10 cm. They vibrate in phase to produce waves of wavelength 5.0 cm. What would be the phase difference between the two waves arriving at a point 20 cm from one source (a) on the line joining the sources and (b) on the perpendicular bisector of the line joining the sources?
Calculate the bulk modulus of air from the following data about a sound wave of wavelength 35 cm travelling in air. The pressure at a point varies between (1.0 × 105 ± 14) Pa and the particles of the air vibrate in simple harmonic motion of amplitude 5.5 × 10−6 m.
The intensity of sound from a point source is 1.0 × 10−8 W m−2 at a distance of 5.0 m from the source. What will be the intensity at a distance of 25 m from the source?
The sound level at a point 5.0 m away from a point source is 40 dB. What will be the level at a point 50 m away from the source?
If the intensity of sound is doubled, by how many decibels does the sound level increase?
A string, fixed at both ends, vibrates in a resonant mode with a separation of 2⋅0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1⋅6 cm. Find the length of the string.
Three sources of sound S1, S2 and S3 of equal intensity are placed in a straight line with S1S2 = S2S3. At a point P, far away from the sources, the wave coming from S2 is 120° ahead in phase of that from S1. Also, the wave coming from S3 is 120° ahead of that from S2. What would be the resultant intensity of sound at P?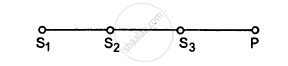
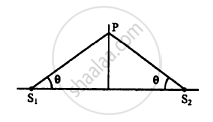
Two sources of sound S1 and S2 vibrate at same frequency and are in phase. The intensity of sound detected at a point P as shown in the figure is I0. (a) If θ equals 45°, what will be the intensity of sound detected at this point if one of the sources is switched off? (b) What will be the answer of the previous part if θ = 60°?
A cylindrical tube, open at both ends, has a fundamental frequency v. The tube is dipped vertically in water so that half of its length is inside the water. The new fundamental frequency is
A piano wire A vibrates at a fundamental frequency of 600 Hz. A second identical wire Bproduces 6 beats per second with it when the tension in A is slightly increased. Find the the ratio of the tension in A to the tension in B.
A train running at 108 km h−1 towards east whistles at a dominant frequency of 500 Hz. Speed of sound in air is 340 m/s. What frequency will a passenger sitting near the open window hear? (b) What frequency will a person standing near the track hear whom the train has just passed? (c) A wind starts blowing towards east at a speed of 36 km h−1. Calculate the frequencies heard by the passenger in the train and by the person standing near the track.
A boy riding on a bicycle going at 12 km h−1 towards a vertical wall whistles at his dog on the ground. If the frequency of the whistle is 1600 Hz and the speed of sound in air is 330 m s−1, find (a) the frequency of the whistle as received by the wall (b) the frequency of the reflected whistle as received by the boy.
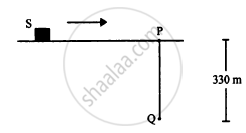
Figure shows a source of sound moving along X-axis at a speed of 22 m s−1continuously emitting a sound of frequency 2.0 kHz which travels in air at a speed of 330 m s−1. A listener Q stands on the Y-axis at a distance of 330 m from the origin. At t = 0, the sources crosses the origin P. (a) When does the sound emitted from the source at P reach the listener Q? (b) What will be the frequency heard by the listener at this instant? (c) Where will the source be at this instant?