Advertisements
Advertisements
प्रश्न
What is the smallest positive phase constant which is equivalent to 7⋅5 π?
उत्तर
Equation of the wave: y = A sin(kx − ωt + Φ)
Here, A is the amplitude, k is the wave number, ω is the angular frequency and Φ is the initial phase.
The argument of the sine is a phase, so the smallest positive phase constant should be
\[\sin\left( 7 . 5\pi \right) = \sin\left( 3 \times 2\pi + 1 . 5\pi \right)\]
\[ = \sin\left( 1 . 5\pi \right)\]
Therefore, the smallest positive phase constant is 1.5π.
APPEARS IN
संबंधित प्रश्न
The wavelengths of two sound waves in air are `81/173`m and `81/170`m. They produce 10 beats per second. Calculate the velocity of sound in air
Can you hear your own words if you are standing in a perfect vacuum? Can you hear your friend in the same conditions?
The voice of a person, who has inhaled helium, has a remarkably high pitch. Explain on the basis of resonant vibration of vocal cord filled with air and with helium.
When we clap our hands, the sound produced is best described by Here p denotes the change in pressure from the equilibrium value.
The bulk modulus and the density of water are greater than those of air. With this much of information, we can say that velocity of sound in air
A man stands before a large wall at a distance of 50.0 m and claps his hands at regular intervals. Initially, the interval is large. He gradually reduces the interval and fixes it at a value when the echo of a clap merges every 3 seconds, find the velocity of sound in air.
The equation of a travelling sound wave is y = 6.0 sin (600 t − 1.8 x) where y is measured in 10−5 m, t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed.
Calculate the bulk modulus of air from the following data about a sound wave of wavelength 35 cm travelling in air. The pressure at a point varies between (1.0 × 105 ± 14) Pa and the particles of the air vibrate in simple harmonic motion of amplitude 5.5 × 10−6 m.
The intensity of sound from a point source is 1.0 × 10−8 W m−2 at a distance of 5.0 m from the source. What will be the intensity at a distance of 25 m from the source?
A particular guitar wire is 30⋅0 cm long and vibrates at a frequency of 196 Hz when no finger is placed on it. The next higher notes on the scale are 220 Hz, 247 Hz, 262 Hz and 294 Hz. How far from the end of the string must the finger be placed to play these notes?
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The sound is detected by moving a detector on the screen ∑ at a distance D(>>λ) from the slit S1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.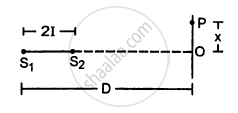
In a standing wave pattern in a vibrating air column, nodes are formed at a distance of 4.0 cm. If the speed of sound in air is 328 m s−1, what is the frequency of the source?
The first overtone frequency of a closed organ pipe P1 is equal to the fundamental frequency of a open organ pipe P2. If the length of the pipe P1 is 30 cm, what will be the length of P2?
A tuning fork produces 4 beats per second with another tuning fork of frequency 256 Hz. The first one is now loaded with a little wax and the beat frequency is found to increase to 6 per second. What was the original frequency of the tuning fork?
A source of sound emitting a 1200 Hz note travels along a straight line at a speed of 170 m s−1. A detector is placed at a distance 200 m from the line of motion of the source. (a) Find the frequency of sound receive by the detector at the instant when the source gets closest to it. (b) Find the distance between the source and the detector at the instant in detects the frequency 1200 Hz. Velocity of sound in air = 340 m s−1.
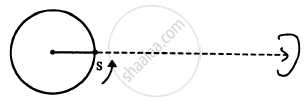
A small source of sound S of frequency 500 Hz is attached to the end of a light string and is whirled in a vertical circle of radius 1.6 m. The string just remains tight when the source is at the highest point. (a) An observer is located in the same vertical plane at a large distance and at the same height as the centre of the circle. The speed of sound in air = 330 m s−1 and g = 10 m s−2. Find the maximum frequency heard by the observer. (b) An observer is situated at a large distance vertically above the centre of the circle. Find the frequency heard by the observer corresponding to the sound emitted by the source when it is at the same height as the centre.
Equation of a plane progressive wave is given by `y = 0.6 sin 2π (t - x/2)`. On reflection from a denser medium its amplitude becomes 2/3 of the amplitude of the incident wave. The equation of the reflected wave is ______.
A transverse wave is represented by y = 2sin (ωt - kx) cm. The value of wavelength (in cm) for which the wave velocity becomes equal to the maximum particle velocity, will be ______.
