Advertisements
Advertisements
प्रश्न
The sound level at a point 5.0 m away from a point source is 40 dB. What will be the level at a point 50 m away from the source?
उत्तर
Let
\[\beta_A\] be the sound level at a point 5 m (= r1) away from the point source and
∴\[\beta_A\]= 40 dB
Sound level is given by:
\[\beta_A = 10 \log_{10} \left( \frac{I_A}{I_0} \right) . \]
\[ \Rightarrow \frac{I_A}{I_0} = {10}^\left( \frac{\beta_A}{10} \right) . . . . . \left( 1 \right)\]
\[ \beta_B = 10 \log_{10} \left( \frac{I_B}{I_o} \right)\]
\[ \Rightarrow \frac{I_B}{I_0} = {10}^\left( \frac{\beta_B}{10} \right) . . . . . \left( 2 \right)\]
\[\text { From } \left( 1 \right) \text { and } \left( 2 \right), \text { we get: }\]
\[ \frac{I_A}{I_B} = {10}^\left( \frac{\beta_A - \beta_B}{10} \right) . . . . \left( 3 \right)\]
\[\text { Also }, \]
\[ \frac{I_A}{I_B} = \frac{r_B^2}{r_A^2} = \left( \frac{50}{5} \right)^2 = {10}^2 . . . . . \left( 4 \right)\]
\[\text { From } \left( 3 \right) \text { and } \left( 4 \right), \text{ we get: }\]
\[ {10}^2 = {10}^\left( \frac{\beta_A - \beta_B}{10} \right) \]
\[ \Rightarrow \frac{\beta_A - \beta_B}{10} = 2 \]
\[ \Rightarrow \beta_A - \beta_B = 20\]
\[ \Rightarrow \beta_B = 40 - 20 = 20 dB\]
\[\beta_A = 10 \log_{10} \left( \frac{I_A}{I_0} \right) . \]
\[ \Rightarrow \frac{I_A}{I_0} = {10}^\left( \frac{\beta_A}{10} \right) . . . . . \left( 1 \right)\]
\[ \beta_B = 10 \log_{10} \left( \frac{I_B}{I_o} \right)\]
\[ \Rightarrow \frac{I_B}{I_0} = {10}^\left( \frac{\beta_B}{10} \right) . . . . . \left( 2 \right)\]
\[\text { From }\left( 1 \right) \text{ and } \left( 2 \right), \text { we get: }\]
\[ \frac{I_A}{I_B} = {10}^\left( \frac{\beta_A - \beta_B}{10} \right) . . . . \left( 3 \right)\]
\[\text { Also }, \]
\[ \frac{I_A}{I_B} = \frac{r_B^2}{r_A^2} = \left( \frac{50}{5} \right)^2 = {10}^2 . . . . . \left( 4 \right)\]
\[\text { From } \left( 3 \right) \text { and } \left( 4 \right), \text { we get: } \]
\[ {10}^2 = {10}^\left( \frac{\beta_A - \beta_B}{10} \right) \]
\[ \Rightarrow \frac{\beta_A - \beta_B}{10} = 2 \]
\[ \Rightarrow \beta_A - \beta_B = 20\]
\[ \Rightarrow \beta_B = 40 - 20 = 20 dB\]
Thus, the sound level of a point 50 m away from the point source is 20 dB.
APPEARS IN
संबंधित प्रश्न
Explain what is Doppler effect in sound
The wavelengths of two sound waves in air are `81/173`m and `81/170`m. They produce 10 beats per second. Calculate the velocity of sound in air
What is the smallest positive phase constant which is equivalent to 7⋅5 π?
The equation \[y = A \sin^2 \left( kx - \omega t \right)\]
represents a wave motion with
If you are walking on the moon, can you hear the sound of stones cracking behind you? Can you hear the sound of your own footsteps?
A source of sound moves towards an observer.
A listener is at rest with respect to the source of sound. A wind starts blowing along the line joining the source and the observer. Which of the following quantities do not change?
(a) Frequency
(b) Velocity of sound
(c) Wavelength
(d) Time period
A man stands before a large wall at a distance of 50.0 m and claps his hands at regular intervals. Initially, the interval is large. He gradually reduces the interval and fixes it at a value when the echo of a clap merges every 3 seconds, find the velocity of sound in air.
Sound waves from a loudspeaker spread nearly uniformly in all directions if the wavelength of the sound is much larger than the diameter of the loudspeaker. (a)Calculate the frequency for which the wavelength of sound in air is ten times the diameter of the speaker if the diameter is 20 cm. (b) Sound is essentially transmitted in the forward direction if the wavelength is much shorter than the diameter of the speaker. Calculate the frequency at which the wavelength of the sound is one tenth of the diameter of the speaker described above. Take the speed of sound to be 340 m/s.
A particular guitar wire is 30⋅0 cm long and vibrates at a frequency of 196 Hz when no finger is placed on it. The next higher notes on the scale are 220 Hz, 247 Hz, 262 Hz and 294 Hz. How far from the end of the string must the finger be placed to play these notes?
If the sound level in a room is increased from 50 dB to 60 dB, by what factor is the pressure amplitude increased?
The two sources of sound, S1 and S2, emitting waves of equal wavelength 20.0 cm, are placed with a separation of 20.0 cm between them. A detector can be moved on a line parallel to S1 S2 and at a distance of 20.0 cm from it. Initially, the detector is equidistant from the two sources. Assuming that the waves emitted by the sources are in detector should be shifted to detect a minimum of sound.
Three sources of sound S1, S2 and S3 of equal intensity are placed in a straight line with S1S2 = S2S3. At a point P, far away from the sources, the wave coming from S2 is 120° ahead in phase of that from S1. Also, the wave coming from S3 is 120° ahead of that from S2. What would be the resultant intensity of sound at P?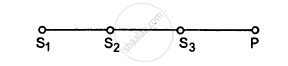
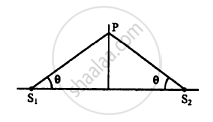
Two sources of sound S1 and S2 vibrate at same frequency and are in phase. The intensity of sound detected at a point P as shown in the figure is I0. (a) If θ equals 45°, what will be the intensity of sound detected at this point if one of the sources is switched off? (b) What will be the answer of the previous part if θ = 60°?
The fundamental frequency of a closed pipe is 293 Hz when the air in it is a temperature of 20°C. What will be its fundamental frequency when the temperature changes to 22°C?
A cylindrical tube, open at both ends, has a fundamental frequency v. The tube is dipped vertically in water so that half of its length is inside the water. The new fundamental frequency is
A sound source, fixed at the origin, is continuously emitting sound at a frequency of 660 Hz. The sound travels in air at a speed of 330 m s−1. A listener is moving along the lien x= 336 m at a constant speed of 26 m s−1. Find the frequency of the sound as observed by the listener when he is (a) at y = − 140 m, (b) at y = 0 and (c) at y = 140 m.
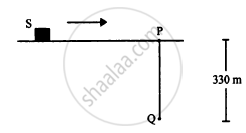
Figure shows a source of sound moving along X-axis at a speed of 22 m s−1continuously emitting a sound of frequency 2.0 kHz which travels in air at a speed of 330 m s−1. A listener Q stands on the Y-axis at a distance of 330 m from the origin. At t = 0, the sources crosses the origin P. (a) When does the sound emitted from the source at P reach the listener Q? (b) What will be the frequency heard by the listener at this instant? (c) Where will the source be at this instant?
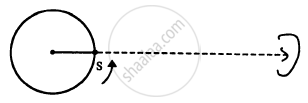
A small source of sound S of frequency 500 Hz is attached to the end of a light string and is whirled in a vertical circle of radius 1.6 m. The string just remains tight when the source is at the highest point. (a) An observer is located in the same vertical plane at a large distance and at the same height as the centre of the circle. The speed of sound in air = 330 m s−1 and g = 10 m s−2. Find the maximum frequency heard by the observer. (b) An observer is situated at a large distance vertically above the centre of the circle. Find the frequency heard by the observer corresponding to the sound emitted by the source when it is at the same height as the centre.