Advertisements
Advertisements
Question
The sound level at a point 5.0 m away from a point source is 40 dB. What will be the level at a point 50 m away from the source?
Solution
Let
\[\beta_A\] be the sound level at a point 5 m (= r1) away from the point source and
∴\[\beta_A\]= 40 dB
Sound level is given by:
\[\beta_A = 10 \log_{10} \left( \frac{I_A}{I_0} \right) . \]
\[ \Rightarrow \frac{I_A}{I_0} = {10}^\left( \frac{\beta_A}{10} \right) . . . . . \left( 1 \right)\]
\[ \beta_B = 10 \log_{10} \left( \frac{I_B}{I_o} \right)\]
\[ \Rightarrow \frac{I_B}{I_0} = {10}^\left( \frac{\beta_B}{10} \right) . . . . . \left( 2 \right)\]
\[\text { From } \left( 1 \right) \text { and } \left( 2 \right), \text { we get: }\]
\[ \frac{I_A}{I_B} = {10}^\left( \frac{\beta_A - \beta_B}{10} \right) . . . . \left( 3 \right)\]
\[\text { Also }, \]
\[ \frac{I_A}{I_B} = \frac{r_B^2}{r_A^2} = \left( \frac{50}{5} \right)^2 = {10}^2 . . . . . \left( 4 \right)\]
\[\text { From } \left( 3 \right) \text { and } \left( 4 \right), \text{ we get: }\]
\[ {10}^2 = {10}^\left( \frac{\beta_A - \beta_B}{10} \right) \]
\[ \Rightarrow \frac{\beta_A - \beta_B}{10} = 2 \]
\[ \Rightarrow \beta_A - \beta_B = 20\]
\[ \Rightarrow \beta_B = 40 - 20 = 20 dB\]
\[\beta_A = 10 \log_{10} \left( \frac{I_A}{I_0} \right) . \]
\[ \Rightarrow \frac{I_A}{I_0} = {10}^\left( \frac{\beta_A}{10} \right) . . . . . \left( 1 \right)\]
\[ \beta_B = 10 \log_{10} \left( \frac{I_B}{I_o} \right)\]
\[ \Rightarrow \frac{I_B}{I_0} = {10}^\left( \frac{\beta_B}{10} \right) . . . . . \left( 2 \right)\]
\[\text { From }\left( 1 \right) \text{ and } \left( 2 \right), \text { we get: }\]
\[ \frac{I_A}{I_B} = {10}^\left( \frac{\beta_A - \beta_B}{10} \right) . . . . \left( 3 \right)\]
\[\text { Also }, \]
\[ \frac{I_A}{I_B} = \frac{r_B^2}{r_A^2} = \left( \frac{50}{5} \right)^2 = {10}^2 . . . . . \left( 4 \right)\]
\[\text { From } \left( 3 \right) \text { and } \left( 4 \right), \text { we get: } \]
\[ {10}^2 = {10}^\left( \frac{\beta_A - \beta_B}{10} \right) \]
\[ \Rightarrow \frac{\beta_A - \beta_B}{10} = 2 \]
\[ \Rightarrow \beta_A - \beta_B = 20\]
\[ \Rightarrow \beta_B = 40 - 20 = 20 dB\]
Thus, the sound level of a point 50 m away from the point source is 20 dB.
APPEARS IN
RELATED QUESTIONS
The equation \[y = A \sin^2 \left( kx - \omega t \right)\]
represents a wave motion with
Two loudspeakers are arranged facing each other at some distance. Will a person standing behind one of the loudspeakers clearly hear the sound of the other loudspeaker or the clarity will be seriously damaged because of the 'collision' of the two sounds in between?
Two tuning forks vibrate with the same amplitude but the frequency of the first is double the frequency of the second. Which fork produces more intense sound in air?
Two sound waves move in the same direction in the same medium. The pressure amplitudes of the waves are equal but the wavelength of the first wave is double the second. Let the average power transmitted across a cross section by the first wave be P1 and that by the second wave be P2. Then
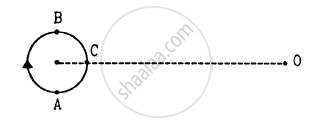
A small source of sounds moves on a circle as shown in figure and an observer is sitting at O. Let \[v_1, v_2, v_3\] be the frequencies heard when the source is at A, B and C respectively.
A listener is at rest with respect to the source of sound. A wind starts blowing along the line joining the source and the observer. Which of the following quantities do not change?
(a) Frequency
(b) Velocity of sound
(c) Wavelength
(d) Time period
A man stands before a large wall at a distance of 50.0 m and claps his hands at regular intervals. Initially, the interval is large. He gradually reduces the interval and fixes it at a value when the echo of a clap merges every 3 seconds, find the velocity of sound in air.
A person can hear sound waves in the frequency range 20 Hz to 20 kHz. Find the minimum and the maximum wavelengths of sound that is audible to the person. The speed of sound is 360 m s−1.
The intensity of sound from a point source is 1.0 × 10−8 W m−2 at a distance of 5.0 m from the source. What will be the intensity at a distance of 25 m from the source?
The noise level in a classroom in absence of the teacher is 50 dB when 50 students are present. Assuming that on the average each student output same sound energy per second, what will be the noise level if the number of students is increased to 100?
A uniform horizontal rod of length 40 cm and mass 1⋅2 kg is supported by two identical wires as shown in figure. Where should a mass of 4⋅8 kg be placed on the rod so that the same tuning fork may excite the wire on left into its fundamental vibrations and that on right into its first overtone? Take g = 10 m s−2.
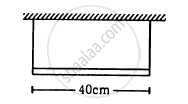
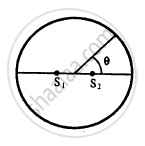
Figure shown two coherent sources S1 and S2 which emit sound of wavelength λ in phase. The separation between the sources is 3λ. A circular wire of large radius is placed in such way that S1,S2 is at the centre of the wire. Find the angular positions θ on the wire for which constructive interference takes place.
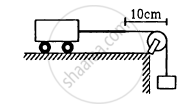
A heavy string is tied at one end to a movable support and to a light thread at the other end as shown in following figure. The thread goes over a fixed pulley and supports a weight to produce a tension. The lowest frequency with which the heavy string resonates is 120 Hz. If the movable support is pushed to the right by 10 cm so that the joint is placed on the pulley, what will be the minimum frequency at which the heavy string can resonate?
Consider the situation shown in the figure.The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 340 m s−1, find the tension in the wire.
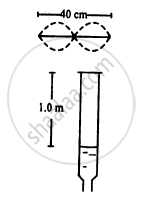
A piano wire A vibrates at a fundamental frequency of 600 Hz. A second identical wire Bproduces 6 beats per second with it when the tension in A is slightly increased. Find the the ratio of the tension in A to the tension in B.
A traffic policeman standing on a road sounds a whistle emitting the main frequency of 2.00 kHz. What could be the apparent frequency heard by a scooter-driver approaching the policeman at a speed of 36.0 km h−1? Speed of sound in air = 340 m s−1.
Two electric trains run at the same speed of 72 km h−1 along the same track and in the same direction with separation of 2.4 km between them. The two trains simultaneously sound brief whistles. A person is situated at a perpendicular distance of 500 m from the track and is equidistant from the two trains at the instant of the whistling. If both the whistles were at 500 Hz and the speed of sound in air is 340 m s−1, find the frequencies heard by the person.
A train running at 108 km h−1 towards east whistles at a dominant frequency of 500 Hz. Speed of sound in air is 340 m/s. What frequency will a passenger sitting near the open window hear? (b) What frequency will a person standing near the track hear whom the train has just passed? (c) A wind starts blowing towards east at a speed of 36 km h−1. Calculate the frequencies heard by the passenger in the train and by the person standing near the track.
A boy riding on a bicycle going at 12 km h−1 towards a vertical wall whistles at his dog on the ground. If the frequency of the whistle is 1600 Hz and the speed of sound in air is 330 m s−1, find (a) the frequency of the whistle as received by the wall (b) the frequency of the reflected whistle as received by the boy.
A transverse wave is represented by y = 2sin (ωt - kx) cm. The value of wavelength (in cm) for which the wave velocity becomes equal to the maximum particle velocity, will be ______.
