Advertisements
Advertisements
Question
A boy riding on a bicycle going at 12 km h−1 towards a vertical wall whistles at his dog on the ground. If the frequency of the whistle is 1600 Hz and the speed of sound in air is 330 m s−1, find (a) the frequency of the whistle as received by the wall (b) the frequency of the reflected whistle as received by the boy.
Solution
Given:
Velocity of sound in air v = 330 ms−1
(a) Frequency of whistle \[n_0\]=1600 Hz
Velocity of source vs = 12 km/h =\[12 \times \frac{5}{18} = \frac{10}{3} {\text { ms }}^{- 1}\]
Velocity of an observer \[v_0\] = 0 ms−1
Frequency of whistle received by wall n =?Frequency of sound received by the observer is given by :
\[n = \frac{v + v_0}{v - v_s} \times n_0\]
On substituting the respective values in the above formula, we get :
\[n = \frac{330 + 0}{330 - \frac{10}{3}} \times 1600 = 1616 \text{ Hz }\]
(b) Here,
Velocity of observer \[v_0\] \[\frac{10}{3} {\text { ms }}^{- 1}\]
Velocity of source vs = 0
Frequency of source \[n_0\]= 1616 Hz
Frequency of sound heard by observer is
\[n = \frac{v + v_0}{v + v_s} \times n_0 \]
On substituting the respective values in the above formula, we get :
\[= \frac{330 + \frac{10}{3}}{330 + 0} \times 1616 = 1632 \text{ Hz }\]
APPEARS IN
RELATED QUESTIONS
A wave is represented by an equation \[y = c_1 \sin \left( c_2 x + c_3 t \right)\] In which direction is the wave going? Assume that \[c_1 , c_2\] \[c_3\] are all positive.
What is the smallest positive phase constant which is equivalent to 7⋅5 π?
The equation \[y = A \sin^2 \left( kx - \omega t \right)\]
represents a wave motion with
Two tuning forks vibrate with the same amplitude but the frequency of the first is double the frequency of the second. Which fork produces more intense sound in air?
The fundamental frequency of a vibrating organ pipe is 200 Hz.
(a) The first overtone is 400 Hz.
(b) The first overtone may be 400 Hz.
(c) The first overtone may be 600 Hz.
(d) 600 Hz is an overtone.
A listener is at rest with respect to the source of sound. A wind starts blowing along the line joining the source and the observer. Which of the following quantities do not change?
(a) Frequency
(b) Velocity of sound
(c) Wavelength
(d) Time period
A steel tube of length 1.00 m is struck at one end. A person with his ear closed to the other end hears the sound of the blow twice, one travelling through the body of the tube and the other through the air in the tube. Find the time gap between the two hearings. Use the table in the text for speeds of sound in various substances.
Sound waves from a loudspeaker spread nearly uniformly in all directions if the wavelength of the sound is much larger than the diameter of the loudspeaker. (a)Calculate the frequency for which the wavelength of sound in air is ten times the diameter of the speaker if the diameter is 20 cm. (b) Sound is essentially transmitted in the forward direction if the wavelength is much shorter than the diameter of the speaker. Calculate the frequency at which the wavelength of the sound is one tenth of the diameter of the speaker described above. Take the speed of sound to be 340 m/s.
A sound wave frequency 100 Hz is travelling in air. The speed of sound in air is 350 m s−1. (a) By how much is the phase changed at a given point in 2.5 ms? (b) What is the phase difference at a given instant between two points separated by a distance of 10.0 cm along the direction of propagation?
The length of the wire shown in figure between the pulley is 1⋅5 m and its mass is 12⋅0 g. Find the frequency of vibration with which the wire vibrates in two loops leaving the middle point of the wire between the pulleys at rest.
Sound with intensity larger than 120 dB appears pain full to a person. A small speaker delivers 2.0 W of audio output. How close can the person get to the speaker without hurting his ears?
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The sound is detected by moving a detector on the screen ∑ at a distance D(>>λ) from the slit S1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.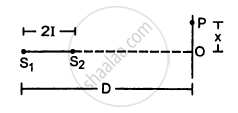
Show that if the room temperature changes by a small amount from T to T + ∆T, the fundamental frequency of an organ pipe changes from v to v + ∆v, where \[\frac{∆ v}{v} = \frac{1}{2}\frac{∆ T}{T} .\]
A piano wire A vibrates at a fundamental frequency of 600 Hz. A second identical wire Bproduces 6 beats per second with it when the tension in A is slightly increased. Find the the ratio of the tension in A to the tension in B.
A tuning fork of frequency 256 Hz produces 4 beats per second with a wire of length 25 cm vibrating in its fundamental mode. The beat frequency decreases when the length is slightly shortened. What could be the minimum length by which the wire we shortened so that it produces no beats with the tuning fork?
A small source of sound oscillates in simple harmonic motion with an amplitude of 17 cm. A detector is placed along the line of motion of the source. The source emits a sound of frequency 800 Hz which travels at a speed of 340 m s−1. If the width of the frequency band detected by the detector is 8 Hz, find the time period of the source.
A boy riding on his bike is going towards east at a speed of 4√2 m s−1. At a certain point he produces a sound pulse of frequency 1650 Hz that travels in air at a speed of 334 m s−1. A second boy stands on the ground 45° south of east from his. Find the frequency of the pulse as received by the second boy.
A person standing on a road sends a sound signal to the driver of a car going away from him at a speed of 72 km h−1. The signal travelling at 330 m s−1 in air and having a frequency of 1600 Hz gets reflected from the body of the car and returns. Find the frequency of the reflected signal as heard by the person.
Which of the following statements are true for wave motion?
