Advertisements
Advertisements
Question
A small source of sound oscillates in simple harmonic motion with an amplitude of 17 cm. A detector is placed along the line of motion of the source. The source emits a sound of frequency 800 Hz which travels at a speed of 340 m s−1. If the width of the frequency band detected by the detector is 8 Hz, find the time period of the source.
Solution
Given:
Amplitude r = 17 cm = \[\frac{17}{100}\]= 0.17 m
Frequency of sound emitted by source f = 800 Hz
Velocity of sound \[v\]= 340 m/s
Frequency band = f2\[-\]f1= 8 Hz
Here,
\[f_2\] and \[f_1\]correspond to the maximum and minimum apparent frequencies (Both will be at the mean position because the velocity is maximum).
\[\text { Now }, f_1 = \left( \frac{340}{340 + v_s} \right)f\]
\[ \text { and } f_2 = \left( \frac{340}{340 - v_s} \right)f\]
\[ \therefore f_2 - f_1 = 8\]
\[ \Rightarrow 8 = \left( \frac{340}{340 - v_s} \right)f - \left( \frac{340}{340 + v_s} \right)f\]
\[ \Rightarrow 8 = 340f\left[ \frac{1}{340 - v_s} - \frac{1}{340 + v_s} \right]\]
\[ \Rightarrow 8 = 340 \times 800 \times \left[ \frac{2 v_s}{{340}^2 - {v_s}^2} \right]\]
\[ \Rightarrow \frac{2 v_s}{{340}^2 - v_s^2} = \frac{8}{340 \times 800}\]
\[ \Rightarrow {340}^2 - {v_s}^2 = 68000 v_s \]
Solving for vs, we get:
\[v_s\]= 1.695 m/s
For SHM:
\[v_s = r\omega\]
\[ \Rightarrow \omega = \left( \frac{1 . 695}{0 . 17} \right) = 10\]
\[ \therefore T = \frac{2\pi}{w} = \frac{\pi}{5} = 0 . 63 \sec\]
APPEARS IN
RELATED QUESTIONS
Explain what is Doppler effect in sound
A wave is represented by an equation \[y = c_1 \sin \left( c_2 x + c_3 t \right)\] In which direction is the wave going? Assume that \[c_1 , c_2\] \[c_3\] are all positive.
The voice of a person, who has inhaled helium, has a remarkably high pitch. Explain on the basis of resonant vibration of vocal cord filled with air and with helium.
At what temperature will the speed of sound be double of its value at 0°C?
The sound level at a point 5.0 m away from a point source is 40 dB. What will be the level at a point 50 m away from the source?
Sound with intensity larger than 120 dB appears pain full to a person. A small speaker delivers 2.0 W of audio output. How close can the person get to the speaker without hurting his ears?
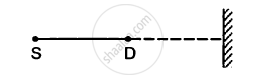
A source of sound S and detector D are placed at some distance from one another. a big cardboard is placed near hte detector and perpendicular to the line SD as shown in figure. It is gradually moved away and it is found that the intensity changes from a maximum to a minimum as the board is moved through a distance of 20 cm. Find the frequency of the sound emitted. Velocity of sound in air is 336 m s−1.
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The sound is detected by moving a detector on the screen ∑ at a distance D(>>λ) from the slit S1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.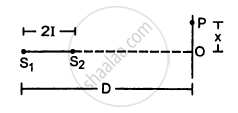
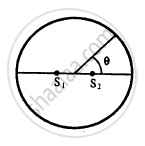
Figure shown two coherent sources S1 and S2 which emit sound of wavelength λ in phase. The separation between the sources is 3λ. A circular wire of large radius is placed in such way that S1,S2 is at the centre of the wire. Find the angular positions θ on the wire for which constructive interference takes place.
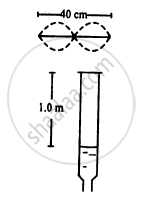
In a standing wave pattern in a vibrating air column, nodes are formed at a distance of 4.0 cm. If the speed of sound in air is 328 m s−1, what is the frequency of the source?
Consider the situation shown in the figure.The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 340 m s−1, find the tension in the wire.
The fundamental frequency of a closed pipe is 293 Hz when the air in it is a temperature of 20°C. What will be its fundamental frequency when the temperature changes to 22°C?
A source of sound with adjustable frequency produces 2 beats per second with a tuning fork when its frequency is either 476 Hz of 480 Hz. What is the frequency of the tuning fork?
A tuning fork produces 4 beats per second with another tuning fork of frequency 256 Hz. The first one is now loaded with a little wax and the beat frequency is found to increase to 6 per second. What was the original frequency of the tuning fork?
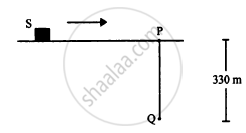
Figure shows a source of sound moving along X-axis at a speed of 22 m s−1continuously emitting a sound of frequency 2.0 kHz which travels in air at a speed of 330 m s−1. A listener Q stands on the Y-axis at a distance of 330 m from the origin. At t = 0, the sources crosses the origin P. (a) When does the sound emitted from the source at P reach the listener Q? (b) What will be the frequency heard by the listener at this instant? (c) Where will the source be at this instant?
For the propagation of longitudinal waves, the medium must have
- elasticity
- mass
- inertia
- force of cohesion
In an experiment to determine the velocity of sound in air at room temperature using a resonance tube, the first resonance is observed when the air column has a length of 20.0 cm for a tuning fork of frequency 400 Hz is used. The velocity of the sound at room temperature is 336 ms-1. The third resonance is observed when the air column has a length of ______ cm.
The speed of a wave in a string is 20 m/s and the frequency is 50 Hz. The phase difference between two points on the string 10 cm apart will be ______.
