Advertisements
Advertisements
प्रश्न
A small source of sound oscillates in simple harmonic motion with an amplitude of 17 cm. A detector is placed along the line of motion of the source. The source emits a sound of frequency 800 Hz which travels at a speed of 340 m s−1. If the width of the frequency band detected by the detector is 8 Hz, find the time period of the source.
उत्तर
Given:
Amplitude r = 17 cm = \[\frac{17}{100}\]= 0.17 m
Frequency of sound emitted by source f = 800 Hz
Velocity of sound \[v\]= 340 m/s
Frequency band = f2\[-\]f1= 8 Hz
Here,
\[f_2\] and \[f_1\]correspond to the maximum and minimum apparent frequencies (Both will be at the mean position because the velocity is maximum).
\[\text { Now }, f_1 = \left( \frac{340}{340 + v_s} \right)f\]
\[ \text { and } f_2 = \left( \frac{340}{340 - v_s} \right)f\]
\[ \therefore f_2 - f_1 = 8\]
\[ \Rightarrow 8 = \left( \frac{340}{340 - v_s} \right)f - \left( \frac{340}{340 + v_s} \right)f\]
\[ \Rightarrow 8 = 340f\left[ \frac{1}{340 - v_s} - \frac{1}{340 + v_s} \right]\]
\[ \Rightarrow 8 = 340 \times 800 \times \left[ \frac{2 v_s}{{340}^2 - {v_s}^2} \right]\]
\[ \Rightarrow \frac{2 v_s}{{340}^2 - v_s^2} = \frac{8}{340 \times 800}\]
\[ \Rightarrow {340}^2 - {v_s}^2 = 68000 v_s \]
Solving for vs, we get:
\[v_s\]= 1.695 m/s
For SHM:
\[v_s = r\omega\]
\[ \Rightarrow \omega = \left( \frac{1 . 695}{0 . 17} \right) = 10\]
\[ \therefore T = \frac{2\pi}{w} = \frac{\pi}{5} = 0 . 63 \sec\]
APPEARS IN
संबंधित प्रश्न
Two tuning forks vibrate with the same amplitude but the frequency of the first is double the frequency of the second. Which fork produces more intense sound in air?
The fundamental frequency of a vibrating organ pipe is 200 Hz.
(a) The first overtone is 400 Hz.
(b) The first overtone may be 400 Hz.
(c) The first overtone may be 600 Hz.
(d) 600 Hz is an overtone.
Ultrasonic waves of frequency 4.5 MHz are used to detect tumour in soft tissue. The speed of sound in tissue is 1.5 km s−1 and that in air is 340 m s−1. Find the wavelength of this ultrasonic wave in air and in tissue.
A sound wave frequency 100 Hz is travelling in air. The speed of sound in air is 350 m s−1. (a) By how much is the phase changed at a given point in 2.5 ms? (b) What is the phase difference at a given instant between two points separated by a distance of 10.0 cm along the direction of propagation?
At what temperature will the speed of sound be double of its value at 0°C?
The length of the wire shown in figure between the pulley is 1⋅5 m and its mass is 12⋅0 g. Find the frequency of vibration with which the wire vibrates in two loops leaving the middle point of the wire between the pulleys at rest.
The intensity of sound from a point source is 1.0 × 10−8 W m−2 at a distance of 5.0 m from the source. What will be the intensity at a distance of 25 m from the source?
A particular guitar wire is 30⋅0 cm long and vibrates at a frequency of 196 Hz when no finger is placed on it. The next higher notes on the scale are 220 Hz, 247 Hz, 262 Hz and 294 Hz. How far from the end of the string must the finger be placed to play these notes?
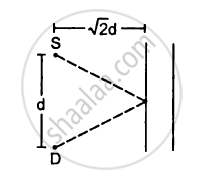
A source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance \[\sqrt{2}d\] from the source and the detector as shown in figure. The source emits a wave of wavelength = d/2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave?
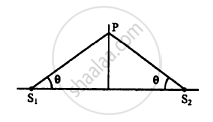
The two sources of sound, S1 and S2, emitting waves of equal wavelength 20.0 cm, are placed with a separation of 20.0 cm between them. A detector can be moved on a line parallel to S1 S2 and at a distance of 20.0 cm from it. Initially, the detector is equidistant from the two sources. Assuming that the waves emitted by the sources are in detector should be shifted to detect a minimum of sound.
Three sources of sound S1, S2 and S3 of equal intensity are placed in a straight line with S1S2 = S2S3. At a point P, far away from the sources, the wave coming from S2 is 120° ahead in phase of that from S1. Also, the wave coming from S3 is 120° ahead of that from S2. What would be the resultant intensity of sound at P?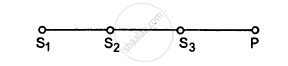
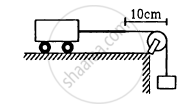
A heavy string is tied at one end to a movable support and to a light thread at the other end as shown in following figure. The thread goes over a fixed pulley and supports a weight to produce a tension. The lowest frequency with which the heavy string resonates is 120 Hz. If the movable support is pushed to the right by 10 cm so that the joint is placed on the pulley, what will be the minimum frequency at which the heavy string can resonate?
Two sources of sound S1 and S2 vibrate at same frequency and are in phase. The intensity of sound detected at a point P as shown in the figure is I0. (a) If θ equals 45°, what will be the intensity of sound detected at this point if one of the sources is switched off? (b) What will be the answer of the previous part if θ = 60°?
The first overtone frequency of a closed organ pipe P1 is equal to the fundamental frequency of a open organ pipe P2. If the length of the pipe P1 is 30 cm, what will be the length of P2?
The fundamental frequency of a closed pipe is 293 Hz when the air in it is a temperature of 20°C. What will be its fundamental frequency when the temperature changes to 22°C?
A sound source, fixed at the origin, is continuously emitting sound at a frequency of 660 Hz. The sound travels in air at a speed of 330 m s−1. A listener is moving along the lien x= 336 m at a constant speed of 26 m s−1. Find the frequency of the sound as observed by the listener when he is (a) at y = − 140 m, (b) at y = 0 and (c) at y = 140 m.
A train running at 108 km h−1 towards east whistles at a dominant frequency of 500 Hz. Speed of sound in air is 340 m/s. What frequency will a passenger sitting near the open window hear? (b) What frequency will a person standing near the track hear whom the train has just passed? (c) A wind starts blowing towards east at a speed of 36 km h−1. Calculate the frequencies heard by the passenger in the train and by the person standing near the track.
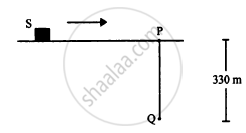
Figure shows a source of sound moving along X-axis at a speed of 22 m s−1continuously emitting a sound of frequency 2.0 kHz which travels in air at a speed of 330 m s−1. A listener Q stands on the Y-axis at a distance of 330 m from the origin. At t = 0, the sources crosses the origin P. (a) When does the sound emitted from the source at P reach the listener Q? (b) What will be the frequency heard by the listener at this instant? (c) Where will the source be at this instant?
For the propagation of longitudinal waves, the medium must have
- elasticity
- mass
- inertia
- force of cohesion
During propagation of a plane progressive mechanical wave ______.
- all the particles are vibrating in the same phase.
- amplitude of all the particles is equal.
- particles of the medium executes S.H.M.
- wave velocity depends upon the nature of the medium.
