Advertisements
Advertisements
प्रश्न
A sound source, fixed at the origin, is continuously emitting sound at a frequency of 660 Hz. The sound travels in air at a speed of 330 m s−1. A listener is moving along the lien x= 336 m at a constant speed of 26 m s−1. Find the frequency of the sound as observed by the listener when he is (a) at y = − 140 m, (b) at y = 0 and (c) at y = 140 m.
उत्तर
Given:
Frequency of sound emitted by the source \[n_0\]= 660 Hz
Velocity of sound in air v = 330 `\text { ms}^\(-)`1
Velocity of observer \[v_0\]= 26 ms−1
Frequency of sound heard by observer n = ?
(a) At y = 140 m:
Frequency of sound heard by the listener, when the source is fixed but the listener is moving towards the source:
\[n = \frac{v + v_0}{v} n_0 \]
Here ,
\[v_0 = v_0 \cos\theta\]
On substituting the values, we get:
\[n = \frac{v + v_0 \cos\theta}{v} n_0 \]
\[ = \frac{330 + 26 \times \frac{140}{364}}{330} \times 660\]
\[ = 340 \times 2 = 680 \text{ Hz }\]
(b) When the observer is at y = 0, the velocity of the observer with respect to the source is zero.
Therefore, he will hear at a frequency of 660 Hz.
(c) When the observer is at y = 140 m:
\[n = \frac{v - v_0}{v} \times n_0 \]
Here,
\[v_0 = v_0 \cos\theta\]
On substituting the values, we get:
\[n = \frac{330 - \frac{26 \times 140}{364}}{330} \times 660\]
\[n = \frac{330 - 10}{330} \times 660 = 640 \text { Hz }\]
APPEARS IN
संबंधित प्रश्न
A tuning fork sends sound waves in air. If the temperature of the air increases, which of the following parameters will change?
When sound wave is refracted from air to water, which of the following will remain unchanged?
An electrically maintained tuning fork vibrates with constant frequency and constant amplitude. If the temperature of the surrounding air increases but pressure remains constant, the produced will have
(a) larger wavelength
(b) larger frequency
(c) larger velocity
(d) larger time period.
Ultrasonic waves of frequency 4.5 MHz are used to detect tumour in soft tissue. The speed of sound in tissue is 1.5 km s−1 and that in air is 340 m s−1. Find the wavelength of this ultrasonic wave in air and in tissue.
A sources of sound operates at 2.0 kHz, 20 W emitting sound uniformly in all directions. The speed of sound in air is 340 m s−1 and the density of air is 1.2 kg m −3. (a) What is the intensity at a distance of 6.0 m from the source? (b) What will be the pressure amplitude at this point? (c) What will be the displacement amplitude at this point?
If the intensity of sound is doubled, by how many decibels does the sound level increase?
A string, fixed at both ends, vibrates in a resonant mode with a separation of 2⋅0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1⋅6 cm. Find the length of the string.
A uniform horizontal rod of length 40 cm and mass 1⋅2 kg is supported by two identical wires as shown in figure. Where should a mass of 4⋅8 kg be placed on the rod so that the same tuning fork may excite the wire on left into its fundamental vibrations and that on right into its first overtone? Take g = 10 m s−2.
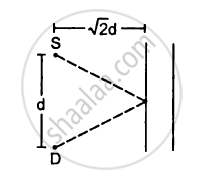
A source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance \[\sqrt{2}d\] from the source and the detector as shown in figure. The source emits a wave of wavelength = d/2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave?
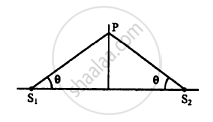
Two sources of sound S1 and S2 vibrate at same frequency and are in phase. The intensity of sound detected at a point P as shown in the figure is I0. (a) If θ equals 45°, what will be the intensity of sound detected at this point if one of the sources is switched off? (b) What will be the answer of the previous part if θ = 60°?
The separation between a node and the next antinode in a vibrating air column is 25 cm. If the speed of sound in air is 340 m s−1, find the frequency of vibration of the air column.
Show that if the room temperature changes by a small amount from T to T + ∆T, the fundamental frequency of an organ pipe changes from v to v + ∆v, where \[\frac{∆ v}{v} = \frac{1}{2}\frac{∆ T}{T} .\]
A boy riding on a bicycle going at 12 km h−1 towards a vertical wall whistles at his dog on the ground. If the frequency of the whistle is 1600 Hz and the speed of sound in air is 330 m s−1, find (a) the frequency of the whistle as received by the wall (b) the frequency of the reflected whistle as received by the boy.
A car moves with a speed of 54 km h−1 towards a cliff. The horn of the car emits sound of frequency 400 Hz at a speed of 335 m s−1. (a) Find the wavelength of the sound emitted by the horn in front of the car. (b) Find the wavelength of the wave reflected from the cliff. (c) What frequency does a person sitting in the car hear for the reflected sound wave? (d) How many beats does he hear in 10 seconds between the sound coming directly from the horn and that coming after the reflection?
A small source of sound S of frequency 500 Hz is attached to the end of a light string and is whirled in a vertical circle of radius 1.6 m. The string just remains tight when the source is at the highest point. (a) An observer is located in the same vertical plane at a large distance and at the same height as the centre of the circle. The speed of sound in air = 330 m s−1 and g = 10 m s−2. Find the maximum frequency heard by the observer. (b) An observer is situated at a large distance vertically above the centre of the circle. Find the frequency heard by the observer corresponding to the sound emitted by the source when it is at the same height as the centre.
Which of the following statements are true for wave motion?
During propagation of a plane progressive mechanical wave ______.
- all the particles are vibrating in the same phase.
- amplitude of all the particles is equal.
- particles of the medium executes S.H.M.
- wave velocity depends upon the nature of the medium.
The speed of a wave in a string is 20 m/s and the frequency is 50 Hz. The phase difference between two points on the string 10 cm apart will be ______.
A transverse wave is represented by y = 2sin (ωt - kx) cm. The value of wavelength (in cm) for which the wave velocity becomes equal to the maximum particle velocity, will be ______.
