Advertisements
Advertisements
प्रश्न
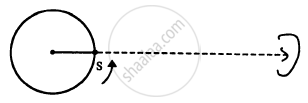
A small source of sound S of frequency 500 Hz is attached to the end of a light string and is whirled in a vertical circle of radius 1.6 m. The string just remains tight when the source is at the highest point. (a) An observer is located in the same vertical plane at a large distance and at the same height as the centre of the circle. The speed of sound in air = 330 m s−1 and g = 10 m s−2. Find the maximum frequency heard by the observer. (b) An observer is situated at a large distance vertically above the centre of the circle. Find the frequency heard by the observer corresponding to the sound emitted by the source when it is at the same height as the centre.
उत्तर
Given:
Frequency of sound emitted by the source \[f_0\] = 500 Hz
Velocity of sound in air v = 330 ms-1
Radius of the circle r = 1.6 m
Frequency of sound heard by the observer v, = ?
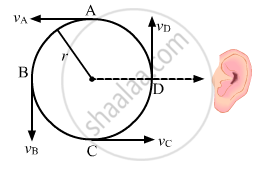
(a)
Velocity of source at highest point of the circle A is given by :
\[v_s = \sqrt{rg}\]=\[\sqrt{10 \times 1 . 6} = 4 \text { m/s }\]
Velocity of sound at C is \[v_c = \sqrt{5rg} = \sqrt{5 \times 1 . 6 \times 10} = 8 . 9 \text { m/s }\]
The frequency of sound heard by the observer when the source is at point C :
\[f_C = \frac{v}{v - v_s} \times f_0\]
Substituting the values, we get :
\[f_C = \frac{330}{330 - 8 . 9} \times 500\]
\[ \Rightarrow f_C = 513 . 85 \text { Hz } \approx 514 \text { Hz }\]
Frequency of sound observed by the observer when the source is at point A :
\[f_A = \frac{v}{v + v_s} \times n_0 \]
\[ = \frac{300}{300 + 4} \times 500 = 494 \text { Hz }\]
Therefore, maximum frequency heard by the observer is 514 Hz.
(b) Velocity at B is given by :
\[v_B = \sqrt{3rg} = \sqrt{3 \times 1 . 6 \times 10} = 6 . 92 \text { m/s }\]
Frequency at B \[\left( f_B \right)\] will be :
\[f_B = \frac{v}{v + v_s} \times f_0 \]
\[ = \frac{330}{330 + 6 . 92} \times 500 = 490 \text { Hz }\]
Frequency at D \[\left( f_D \right)\] will be :
\[f_D = \frac{v}{v - v_s} \times f_0 \]
\[ = \frac{330}{330 - 6 . 92} \times 500 = 511 \text{ Hz }\]
APPEARS IN
संबंधित प्रश्न
A string clamped at both ends vibrates in its fundamental mode. Is there any position (except the ends) on the string which can be touched without disturbing the motion? What if the string vibrates in its first overtone?
If you are walking on the moon, can you hear the sound of stones cracking behind you? Can you hear the sound of your own footsteps?
A tuning fork sends sound waves in air. If the temperature of the air increases, which of the following parameters will change?
When two waves with same frequency and constant phase difference interfere,
When you speak to your friend, which of the following parameters have a unique value in the sound produced?
A man stands before a large wall at a distance of 50.0 m and claps his hands at regular intervals. Initially, the interval is large. He gradually reduces the interval and fixes it at a value when the echo of a clap merges every 3 seconds, find the velocity of sound in air.
Find the minimum and maximum wavelengths of sound in water that is in the audible range (20−20000 Hz) for an average human ear. Speed of sound in water = 1450 m s−1.
The equation of a travelling sound wave is y = 6.0 sin (600 t − 1.8 x) where y is measured in 10−5 m, t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed.
A sources of sound operates at 2.0 kHz, 20 W emitting sound uniformly in all directions. The speed of sound in air is 340 m s−1 and the density of air is 1.2 kg m −3. (a) What is the intensity at a distance of 6.0 m from the source? (b) What will be the pressure amplitude at this point? (c) What will be the displacement amplitude at this point?
The intensity of sound from a point source is 1.0 × 10−8 W m−2 at a distance of 5.0 m from the source. What will be the intensity at a distance of 25 m from the source?
Sound with intensity larger than 120 dB appears pain full to a person. A small speaker delivers 2.0 W of audio output. How close can the person get to the speaker without hurting his ears?
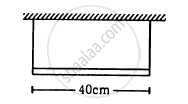
A uniform horizontal rod of length 40 cm and mass 1⋅2 kg is supported by two identical wires as shown in figure. Where should a mass of 4⋅8 kg be placed on the rod so that the same tuning fork may excite the wire on left into its fundamental vibrations and that on right into its first overtone? Take g = 10 m s−2.
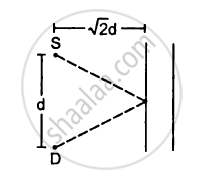
A source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance \[\sqrt{2}d\] from the source and the detector as shown in figure. The source emits a wave of wavelength = d/2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave?
Three sources of sound S1, S2 and S3 of equal intensity are placed in a straight line with S1S2 = S2S3. At a point P, far away from the sources, the wave coming from S2 is 120° ahead in phase of that from S1. Also, the wave coming from S3 is 120° ahead of that from S2. What would be the resultant intensity of sound at P?
In a standing wave pattern in a vibrating air column, nodes are formed at a distance of 4.0 cm. If the speed of sound in air is 328 m s−1, what is the frequency of the source?
A source of sound with adjustable frequency produces 2 beats per second with a tuning fork when its frequency is either 476 Hz of 480 Hz. What is the frequency of the tuning fork?
Show that if the room temperature changes by a small amount from T to T + ∆T, the fundamental frequency of an organ pipe changes from v to v + ∆v, where \[\frac{∆ v}{v} = \frac{1}{2}\frac{∆ T}{T} .\]
A piano wire A vibrates at a fundamental frequency of 600 Hz. A second identical wire Bproduces 6 beats per second with it when the tension in A is slightly increased. Find the the ratio of the tension in A to the tension in B.
During propagation of a plane progressive mechanical wave ______.
- all the particles are vibrating in the same phase.
- amplitude of all the particles is equal.
- particles of the medium executes S.H.M.
- wave velocity depends upon the nature of the medium.
